内容
今回は,空気を蹴って体を浮かすために必要な蹴る速さを求めます. ※ワンピースで月歩(げっぽう)という技があります.月歩は,空気を蹴って体を浮かせる技です.
簡易モデル
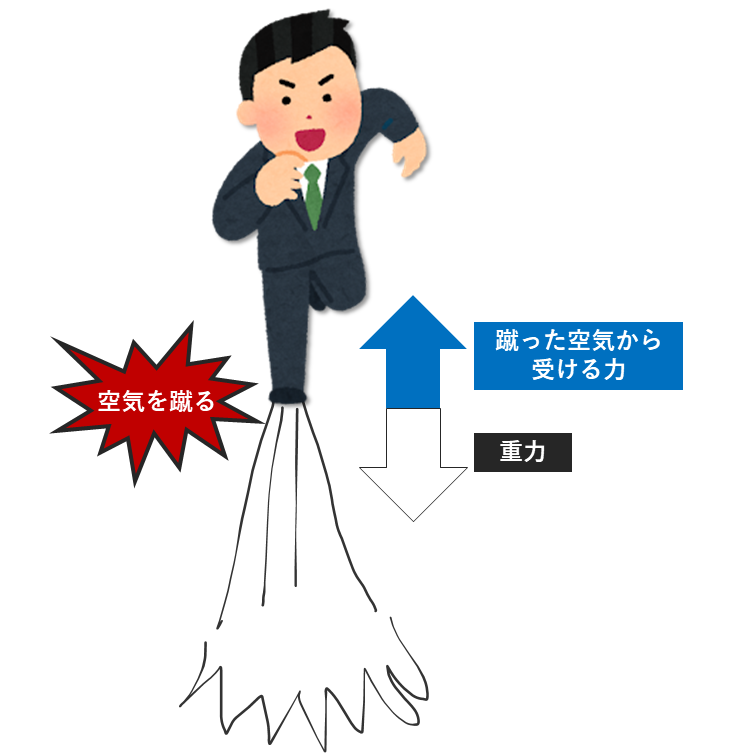
月歩の簡易モデルを説明します.上図に示すように,人が空気を蹴ることを考えます. 蹴られる空気は直方体状であるとし,形状は全く変わらないとします.(空気の塊を1つの剛体とみなすイメージです) 直方体外の空気の影響を全く受けないとします.力はすべて上下方向(\(z\)方向としましょう)に働くとします.蹴りの加速度は一定とします.また,浮力や空気抵抗, 空気の膨張圧縮等の物理はすべて無視します.
計算
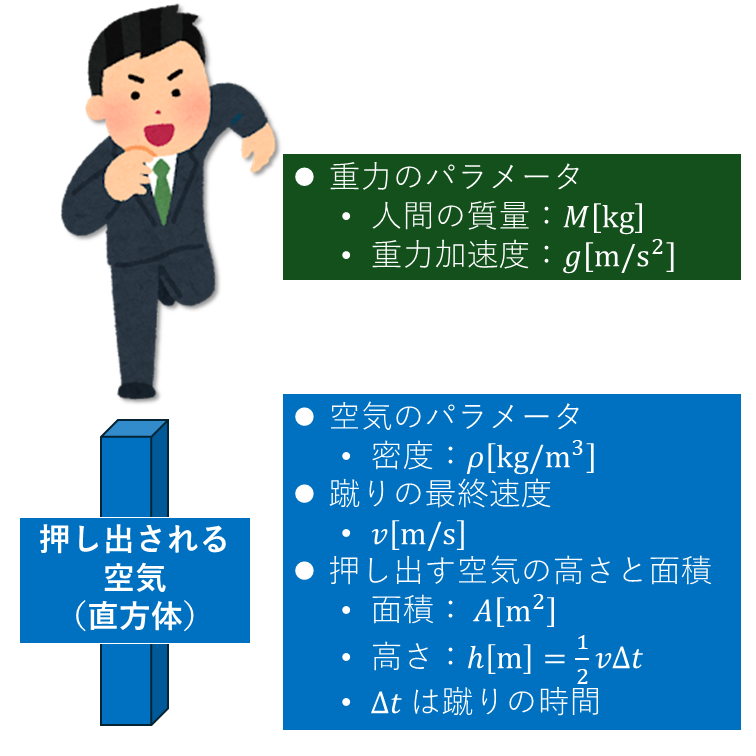
浮く条件を「重力」=「空気を蹴った時の空気から受ける力」とし,浮くために必要な蹴る速さ(蹴り終わり=空気の塊と足が離れる瞬間の最高速度)を計算します.重力は,上図のパラメータを使うと \[ F=Mg \] です.空気を蹴った時の空気から受ける力は,上図のパラメータを使うと \[ F=\rho Aha ~~~(\rho Ah が質量) \] となります.ただし,\(a\) は加速度です.加速度 \(a\) は蹴りの最高速度を \(v\)、蹴りのモーションの時間を \(\Delta t\) とすると \[ a=\frac{v}{\Delta t} \] と書けます.上記の結果より, \[ Mg=\rho Ah\frac{v}{\Delta t} \] となり,\(h=1/2v\Delta t\) を用いると \[ Mg=\frac{1}{2}\rho Av^2 \] となります.\(v\) について解くと, \[ v=\sqrt{\frac{2Mg}{\rho A}} \] が得られます.ここでは,超ざっくりとした計算をするので(特に A は本当の値がよくわからないので)2 のファクターは無視します.すると、 \[ v\sim\sqrt{\frac{Mg}{\rho A}} \] となります.
計算
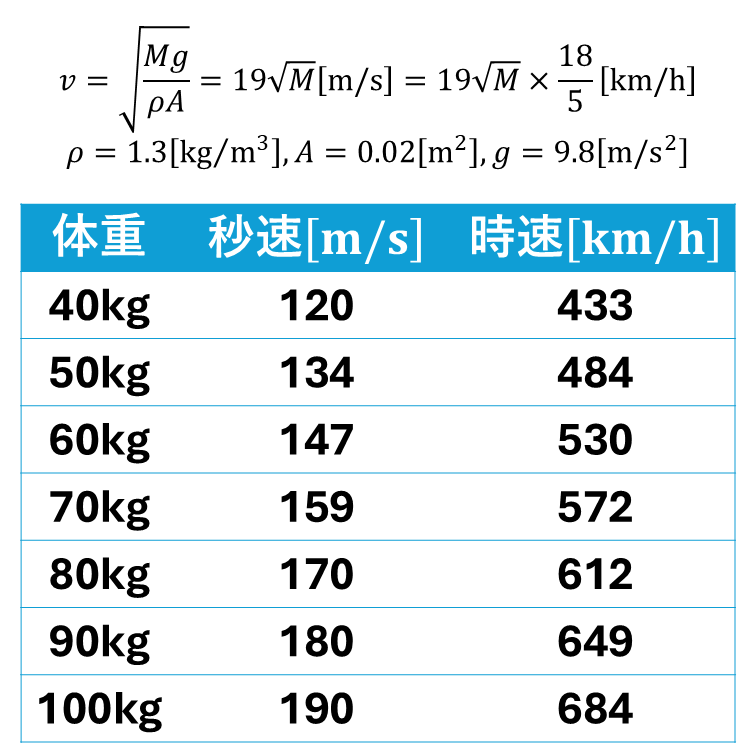
上図に各体重の必要な蹴る速さを示します.パラメータ \(A\) はえいやで決めました.自分の足のサイズこれくらいかな~?と思って与えました.うーん、月歩は非現実的ですね笑