鏡像効果 part.2

ポテンシャル計算

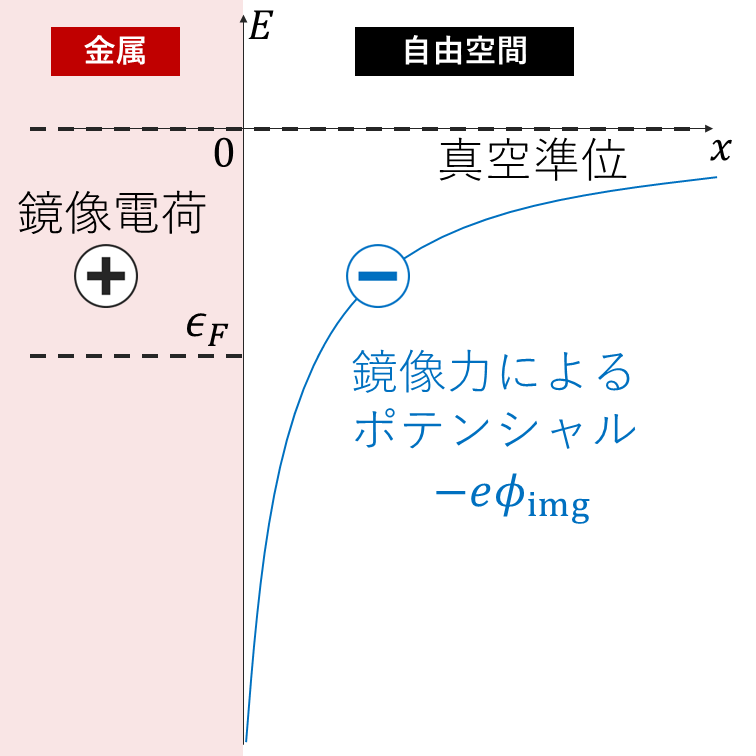
    上図に示す系で，自由空間中の電子は金属中に正の電荷，すなわち鏡像電荷を誘起します．（実際は，電子が動いてバックグラウンドの正の電荷が見える）電子が位置 \(x\) に存在する場合の鏡像力は， \[ F_\mathrm{img}(x)=-\frac{e^2}{4\pi\epsilon_0(2x)^2}=-\frac{e^2}{16\pi\epsilon_0x^2} \] となります． ここで，保存力 \(F\) とポテンシャル \(U\) は，\(F=-\nabla U\) の関係を満たします． したがって，鏡像力による電子が感じるポテンシャルは上式を積分することにより得られます．： \[ U_\mathrm{img}=-e\phi_\mathrm{img}(x)=-\int\left[-\frac{e^2}{16\pi\epsilon_0x^2}\right]dx=-\frac{e^2}{16\pi\epsilon_0x} \]

    上の計算でポテンシャルが得られました．金属側のポテンシャルが低くなっているため，電子は金属側に引き寄せられます．以下では，上記の系に対し"電子を金属から引き抜く方向に外部電場を印加した場合"の現象について考えます．

ショットキー効果

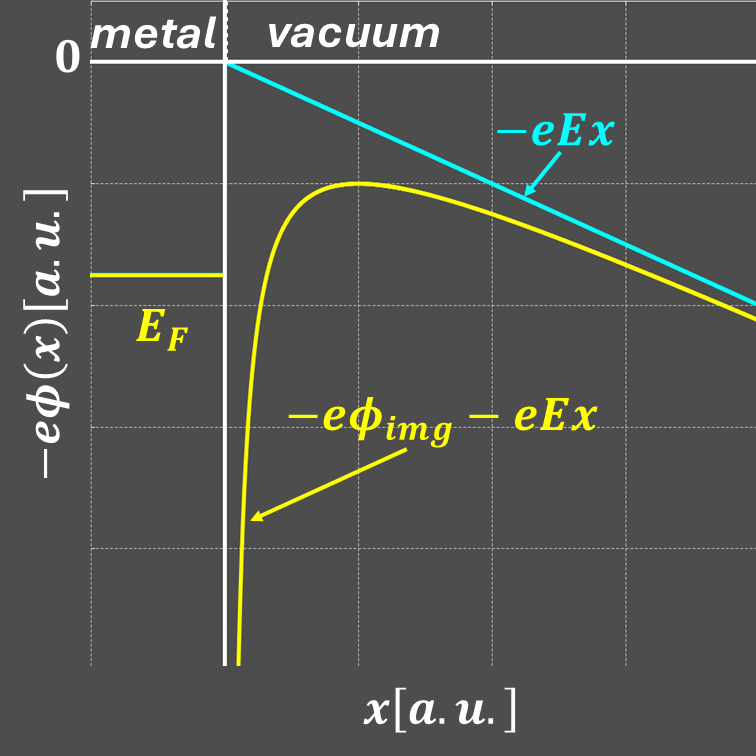
    金属に一様な外部電場 \(E(\geq 0)\) を印加し，金属から電子を引き出すことを考えます．このときの電子が感じるポテンシャルを上図に示します． 上図の水色の線は，外部電場のみを考慮した場合の電子が感じるポテンシャルです． 一方で，黄色の線は，外部電場と鏡像効果の両方を考慮した場合の電子が感じるポテンシャルです． 水色の線と黄色の線を比較すると，鏡像効果を考慮したほうがポテンシャル ー 言い換えると，金属表面から電子を放出させる際の障壁 ー が低くなっていることがわかります．このように外部電場と鏡像効果の組み合わせで，障壁が低下することを「ショットキー効果」あるいは「ショットキー障壁低下」と呼びます．

    では，どのくらい障壁は低下するのでしょうか？実際に計算してみましょう．上図の黄色の線の極大点の \(x\) 座標は， \[ \frac{d}{dx}\left(-\frac{e^2}{16\pi\epsilon_0x}-eEx\right)=0 \] より計算できます．上式の微分を実行すると， \[ \frac{e^2}{16\pi\epsilon_0x^2}-eE=0 \] となり，\(x\) について解けば， \[ x = \sqrt{\frac{e}{16\pi\epsilon_0E}} \] が得られます．上の \(x\) を電子が感じるポテンシャルに代入すれば，障壁のピークが得られます．

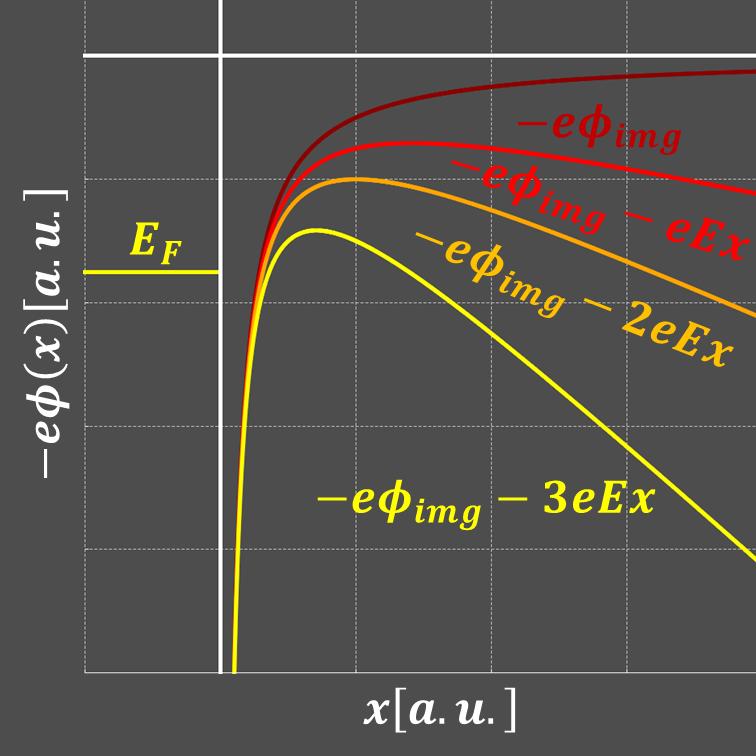
    外部電場 \(E\) がゼロの場合は鏡像効果のみの場合に一致し，障壁のピークは無限遠になります．一方，上図に示すように，外部電場が大きくするにつれ障壁のピークは金属側に近づいていきます．また，外部電場が大きくなるほど，障壁も低くなります．これにより，電子が金属から引き抜かれやすくなります．