トーマス・フェルミ遮蔽

3次元系における遮蔽されたポテンシャルの導出

    3次元で自由電子ガスが存在する空間ー例えば，金属や半導体のバルクーについて考えます．以下では，この空間に正の点電荷 \(q\) を置いた時にできるポテンシャルを計算します．（導出の後に，電荷の符号を反転させたものについて議論します）ただし，正の点電荷は \(\mathbf{r}=(0,0,0)\) にあるとします．また，系は低温で熱平衡状態にあるとします．

    今考えている系で電場をつくる電荷は，正の点電荷 \(q\) と正の点電荷の電場を打ち消すように誘起された電荷です．この場合のポアソン方程式は， \[\nabla^2 \phi(r)=-\frac{1}{\epsilon}\left(q\delta(r)+\rho_\mathrm{ind}(r)\right)\] です．ここで，\(\phi(r)\) は遮蔽効果を考慮したポテンシャル，\(\epsilon\) は物質中の誘電率, \(\rho_\mathrm{ind}\) は正の点電荷によって誘起された電荷の密度（正の点電荷に引き寄せられた電子）です．また，系に球対称性があるため，変数の位置座標 \(\mathbf{r}\) を原点からの距離 \(r\) で書いています．

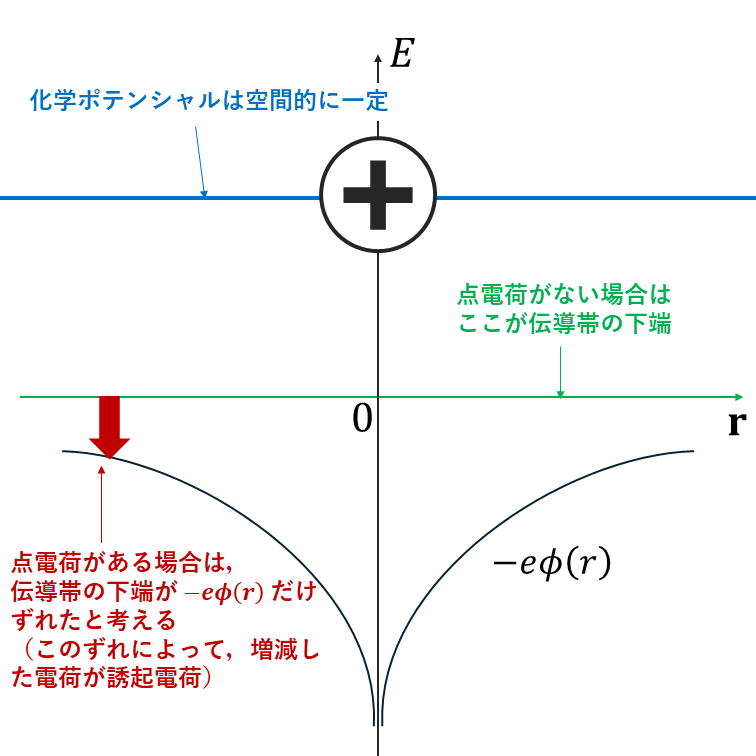
    上式の誘起電荷密度 \(\rho_\mathrm{ind}\) を"何かしらの方法"で与えることができれば，\(\phi(r)\) を計算することができます．その"何かしらの方法"をこの段落で説明します．ここが今回の肝です！ 上図に示すように，熱平衡状態では化学ポテンシャルは空間的に一定です．一方，金属や半導体中の伝導帯の下端のエネルギーは，正の点電荷と誘起電荷により各位置で \(-e\phi(r)\) だけシフトしています．別の言い方をすると，\(\mu=E_F(r)-e\phi(r)➡E_F(r)=\mu+e\phi(r)\) のように，フェルミエネルギーが各位置でシフトしています．このシフトにより，電荷密度が変化します．誘起電荷密度は，正の点電荷が存在する場合の電荷密度分布から，正の点電荷が存在しない場合の電荷密度分布の差です．したがって，誘起電荷密度は， \[\scriptsize \begin{split} \rho_\mathrm{ind}(r)&=-e\left[\int_{-\infty}^\infty f(E)D(E-(-e\phi(r)))dE-\int_{-\infty}^\infty f(E)D(E)dE\right]\\ &=-e\left[\int_{-\infty}^\infty f(E)D(E+e\phi(r))dE-\int_{-\infty}^\infty f(E)D(E)dE\right] \end{split} \] と書けます．上式右辺の第一項が点電荷が存在する場合の電荷密度分布，第二項が点電荷が存在しない場合の電荷密度分布です．

    上式を計算していきましょう．まず，フェルミ分布関数を低温近似でステップ関数とし，状態密度にスピンを考慮した3次元の自由電子の場合の式 \(D(E)=\frac{1}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{E}\) を代入し，積分を実行すれば， \[\scriptsize \begin{split} &\rho_\mathrm{ind}(r)\\ &=-e\left[\int_{-e\phi(r)}^{E_F} \frac{1}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{E+e\phi(r)}dE-\int_0^{E_F} \frac{1}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{E}dE\right]\\ &=-\frac{e}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\left[\frac{2}{3}\sqrt{E_F+e\phi(r)}^3-\frac{2}{3}\sqrt{E_F}^3\right]\\ &=-\frac{e}{3\pi^2}\left(\frac{2m^*E_F}{\hbar^2}\right)^{\frac{3}{2}}\left[\sqrt{1+\frac{e\phi(r)}{E_F}}^3-1\right] \end{split} \] となります．ただし，\(m^*\) は有効質量，\(E_F\) はフェルミエネルギー（0K においては化学ポテンシャルと同じ値）です．また今の場合，\(E+e\phi(r)\) は常に正になります．（上図参照）ここで，\(\frac{e\phi(r)}{E_F} \ll 1\) であるとし，上式を1次の項までテーラー展開すると， \[ \begin{split} \rho_\mathrm{ind}(r) &=-\frac{e}{3\pi^2}\left(\frac{2m^*E_F}{\hbar^2}\right)^{\frac{3}{2}}\left[1+\frac{3}{2}\frac{e\phi(r)}{E_F}-1\right]\\ &=-\frac{e}{3\pi^2}\left(\frac{2m^*E_F}{\hbar^2}\right)^{\frac{3}{2}}\times \frac{3}{2}\frac{e\phi(r)}{E_F} \end{split} \] となります．正の点電荷が存在しない場合の電荷密度が \(\rho_0=-\frac{e}{3\pi^2}\left(\frac{2m^*E_F}{\hbar^2}\right)^{\frac{3}{2}}\) ですので，上式は \[ \begin{split} \rho_\mathrm{ind}(r)=\frac{3e\rho_0}{2E_F} \phi(r) \end{split} \] となります．上式の通り，トーマス・フェルミ近似において，誘起電荷密度は遮蔽効果を考慮したポテンシャルに比例します．

    さて，誘起電荷密度が与えられたので，ポアソン方程式： \[\nabla^2 \phi(r)=-\frac{1}{\epsilon}\left(q\delta(r)+\frac{3e\rho_0}{2E_F} \phi(r)\right)\] をフーリエ変換を利用して解いていきましょう．上式右辺の誘起電荷密度項を左辺に移項すると， \[\left(\nabla^2+\frac{3e\rho_0}{2\epsilon E_F}\right) \phi(r)=-\frac{q}{\epsilon}\delta(r)\] と書けます．上式の \(\phi(r)\) および \(\delta(r)\) をフーリエ変換した形： \[\phi(r)=\frac{1}{(2\pi)^3}\int \Phi(k) e^{-i\mathbf{k}\cdot \mathbf{r}}d\mathbf{k}\] \[\delta(r)=\frac{1}{(2\pi)^3}\int e^{-i\mathbf{q}\cdot \mathbf{r}}d\mathbf{q}\] と書きかえると， \[ \begin{split} &\left(\nabla^2+\frac{3e\rho_0}{2\epsilon E_F}\right) \frac{1}{(2\pi)^3}\int \Phi(k) e^{-i\mathbf{k}\cdot \mathbf{r}}d\mathbf{k}\\ &=-\frac{q}{\epsilon}\frac{1}{(2\pi)^3}\int e^{-i\mathbf{q}\cdot \mathbf{r}}d\mathbf{q} \end{split} \] となります．上式左辺の微分演算子を被積分関数に演算すると， \[ \begin{split} &\frac{1}{(2\pi)^3}\int \left(-k^2+\frac{3e\rho_0}{2\epsilon E_F}\right) \Phi(k) e^{-i\mathbf{k}\cdot \mathbf{r}}d\mathbf{k}\\ &=-\frac{q}{\epsilon}\frac{1}{(2\pi)^3}\int e^{-i\mathbf{q}\cdot \mathbf{r}}d\mathbf{q} \end{split} \] となり，両辺比較すると（あるいは，両辺 \(e^{i\mathbf{k'}\cdots\mathbf{r}}をかけて全空間積分してもよい\)） \[\Phi(k)=\frac{q}{\epsilon}\frac{1}{k^2-\frac{3e\rho_0}{2\epsilon E_F}}\] が得られます．式を見やすくするために，上式右辺の \(\frac{3e\rho_0}{2\epsilon E_F}\) を \(-k_s^2\) と置き換えてみると，(\(-\) をつけるのは，今の場合 \(\rho_0\) が電子密度であり，\(\rho_0 < 0\) であるため) \[\Phi(k)=\frac{q}{\epsilon}\frac{1}{k^2+k_s^2}\] と書けます．あとは，フーリエ変換して，実空間に戻すだけです．上のフーリエ成分を，フーリエ変換形の \(\phi(r)\) に代入すると， \[ \begin{split} \phi(r)&=\frac{1}{(2\pi)^3}\int \frac{q}{\epsilon}\frac{1}{k^2+k_s^2} e^{-i\mathbf{k}\cdot \mathbf{r}}d\mathbf{k}\\ &=\frac{q}{\epsilon}\frac{1}{(2\pi)^3}\int \frac{1}{k^2+k_s^2} e^{-i\mathbf{k}\cdot \mathbf{r}}d\mathbf{k} \end{split} \] となり，極座標表示をし，\(\phi\) および \(\theta\) の積分を順に実行すると， \[ \begin{split} &\phi(r)\\ &=\frac{q}{\epsilon}\frac{1}{(2\pi)^3}\int_0^\infty \int_0^\pi \int_0^{2\pi} \frac{e^{-ikr\cos \theta}}{k^2+k_s^2} k^2\sin \theta dk d\theta d\phi\\ &=\frac{q}{\epsilon}\frac{1}{(2\pi)^3}2\pi \int_0^\infty \int_0^\pi \frac{k^2}{k^2+k_s^2} e^{-ikr\cos\theta}\sin \theta dk d\theta\\ &=\frac{q}{\epsilon}\frac{1}{(2\pi)^2} \int_0^\infty \frac{k^2}{k^2+k_s^2} \frac{1}{-ikr}\left(e^{-ikr}-e^{ikr}\right)dk\\ &=\frac{q}{\epsilon}\frac{i}{(2\pi)^2}\frac{1}{r}\int_0^\infty \frac{k}{k^2+k_s^2} \left(e^{-ikr}-e^{ikr}\right)dk \end{split} \] となります．ここで，上式の積分を１つにまとめると， \[ \begin{split} &\phi(r)\\&=\frac{q}{\epsilon}\frac{i}{(2\pi)^2}\frac{1}{r}\left[\int_0^\infty\frac{ke^{-ikr}}{k^2+k_s^2} dk - \int_0^\infty\frac{ke^{ikr}}{k^2+k_s^2} dk\right]\\ &=\frac{q}{\epsilon}\frac{i}{(2\pi)^2}\frac{1}{r}\left[\int_{-\infty}^0\frac{-ke^{ikr}}{k^2+k_s^2} dk - \int_0^\infty\frac{ke^{ikr}}{k^2+k_s^2} dk\right]\\ &=-\frac{q}{\epsilon}\frac{i}{(2\pi)^2}\frac{1}{r}\int_{-\infty}^\infty\frac{k}{k^2+k_s^2} e^{ikr}dk\\ &=-\frac{q}{\epsilon}\frac{i}{(2\pi)^2}\frac{1}{r}\int_{-\infty}^\infty\frac{1}{2}\left[\frac{1}{k+ik_s}+\frac{1}{k-ik_s}\right] e^{ikr}dk \end{split} \] となります．上式の積分は留数定理により実行します．積分経路は，\(r>0\) であるため下図に示す通り上半面のみです．

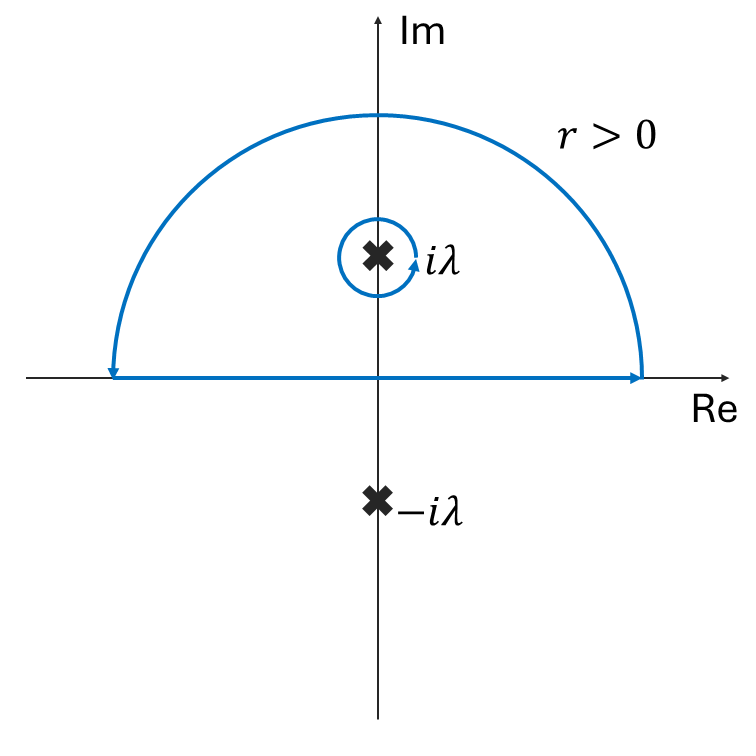
    上半面積分を実行すると， \[ \begin{split} \phi(r)&=-\frac{q}{\epsilon}\frac{i}{(2\pi)^2}\frac{1}{r}\frac{1}{2}2\pi i\mathrm{Res}(ik_s)\\ &=\frac{q}{4\pi\epsilon}\frac{e^{-k_s r}}{r} \end{split} \] となります．最後に，\(\lambda=\frac{1}{k_s}\) と書き直せば， \[ \begin{split} \phi(r)&=\frac{q}{4\pi\epsilon}\frac{e^{-\frac{r}{\lambda}}}{r} \end{split} \] が得られます．\(\lambda\) は遮蔽長です．\(q\) の符号を反転させれば，負の点電荷の場合の式になります．（負の点電荷の場合，周りの電子が遠ざかって，バックグラウンドの正の電荷に遮蔽されます）以下にいくつかの表現を示します． \[ \begin{split} \lambda^2&=-\frac{2\epsilon E_F}{3e\rho_0}~~~(表現１)\\ &=\frac{2\epsilon E_F}{3e^2n_0}~~~(表現２, \rho_0=-en_0)\\ &=-\frac{2\epsilon E_F}{3e}\times\left(-\frac{3\pi^2}{e}\left(\frac{\hbar^2}{2m^*E_F}\right)^{\frac{3}{2}}\right)\\ &=\frac{2\pi^2\epsilon E_F}{e^2}\left(\frac{\hbar^2}{2m^*E_F}\right)^{\frac{3}{2}}~~~(表現３)\\ &=\frac{2\pi^2\epsilon}{e^2}\frac{\hbar^2 k_F^2}{2m^*}k_F^{-3}~~~(k_F=\frac{\sqrt{2m^*E_F}}{\hbar})\\ &=\frac{\pi^2\hbar^2\epsilon}{m^*e^2k_F}~~~(表現４) \end{split} \] \[ \rho_0=-\frac{e}{3\pi^2}\left(\frac{2m^*E_F}{\hbar^2}\right)^{\frac{3}{2}} \]

数式の解説

    遮蔽効果を考慮したポテンシャル： \[ \phi(r)=\frac{q}{4\pi\epsilon}\frac{e^{-\frac{r}{\lambda}}}{r} \] について解説します．点電荷から遮蔽長 \(\lambda\) だけ離れると，電場が届かなくなると考えます．（数式的には電場の強さは0より大きいですが）\(\lambda\rightarrow\infty\)とすると， \[ \phi(r)=\frac{q}{4\pi\epsilon}\frac{1}{r} \] となり，通常のクーロンポテンシャル（bare potential）の形になります．遮蔽長が無限大ということは，遮蔽されないということです．

    遮蔽長 \(\lambda\) について考えます．上の表現４ですと， \[ \lambda^2=\frac{\pi^2\hbar^2\epsilon}{m^*e^2k_F} \] と表されます．（分散関係が \(E=\frac{\hbar^2k^2}{2m^*}\) である系に対して成り立ちます）電子密度が高い系では，それに伴いフェルミ波数 \(k_F\) も大きくなり，遮蔽長が短くなります．つまり，（当然ですが...）電子密度が高くなると遮蔽は強くなります．

    同様に有効質量が大きいほど，遮蔽は強くなります．これは，有効質量が大きいほど状態密度が大きくなり，誘起される電荷量が増加するためです．（このページの導出と直接的な関係はありませんが，運動エネルギーが小さいほどポテンシャルに束縛されやすくなる効果とみることもできます．量子論的な解法を使うとこのイメージがつきます．）

    一方，誘電率が高いと遮蔽長は長くなります．これは，誘起される電荷（ここでは N 個の電子のうちの１つ）は，点電荷と他の電荷（N-1 個の電子）の電場によって誘起されますが，これらからの電場が誘電率が高いと弱められてしまうためです．

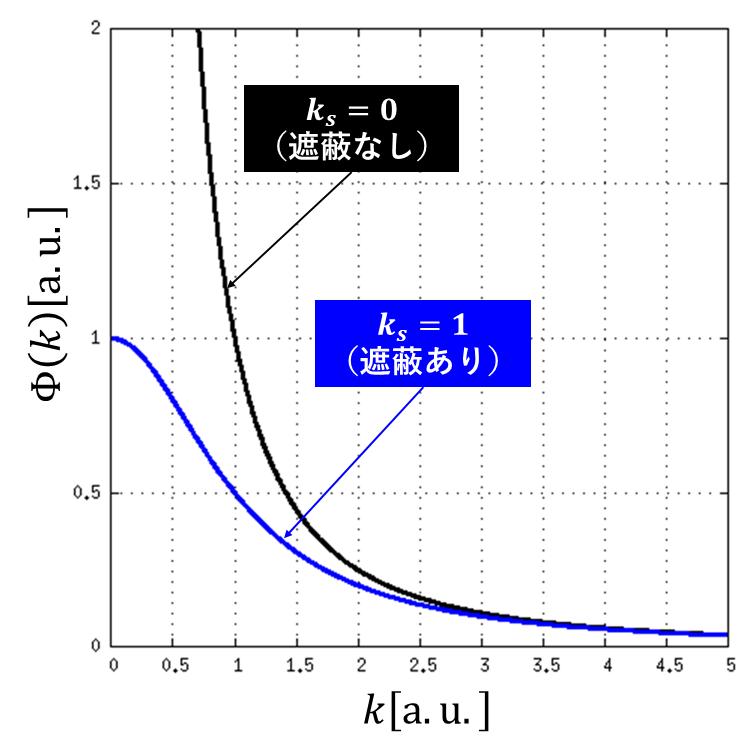
    続いて，ポテンシャルのフーリエ成分について考えてみましょう．式： \[\Phi(k)=\frac{q}{\epsilon}\frac{1}{k^2+k_s^2}\] を， \[\Phi(k)=\frac{q}{\epsilon}\frac{1}{k^2}\frac{1}{1+\frac{k_s^2}{k^2}}=\frac{q}{\epsilon}\frac{1}{k^2}\frac{1}{\epsilon (k)}\] と書き換えます．上式の \(\epsilon (k)=1+\frac{k_s^2}{k^2}\) は誘電関数といいます．ポテンシャルのあるフーリエ成分 \(\frac{1}{k^2}\) をどの程度弱くするか（=遮蔽するか）を表しています．上図に遮蔽ありの場合となしの場合のポテンシャルのフーリエ成分を示します．\(k\) が小さい領域では，遮蔽効果によってフーリエ成分が大きく減少しているいことがお分かりになると思います．実空間に焼きなおすと，ポテンシャルの緩やかな部分は遮蔽されやすいということです．一方で，\(k\) が大きい，すなわち高波数（あるいは短波長）領域では，黒線と青線が重なっており，あまり遮蔽されていないことがわかります．ポテンシャルが急峻に変化する部分は遮蔽しにくいのです．

    上の \(k_s\) は，遮蔽波数と呼ばれます．波数空間では，遮蔽波数が遮蔽されるされないの目安になります．遮蔽波数が大きいほうが，より広い範囲のポテンシャルのフーリエ成分を遮蔽できます．（実空間における遮蔽長の話を，波数空間で議論するとこのような言い方になります．）

数値計算結果

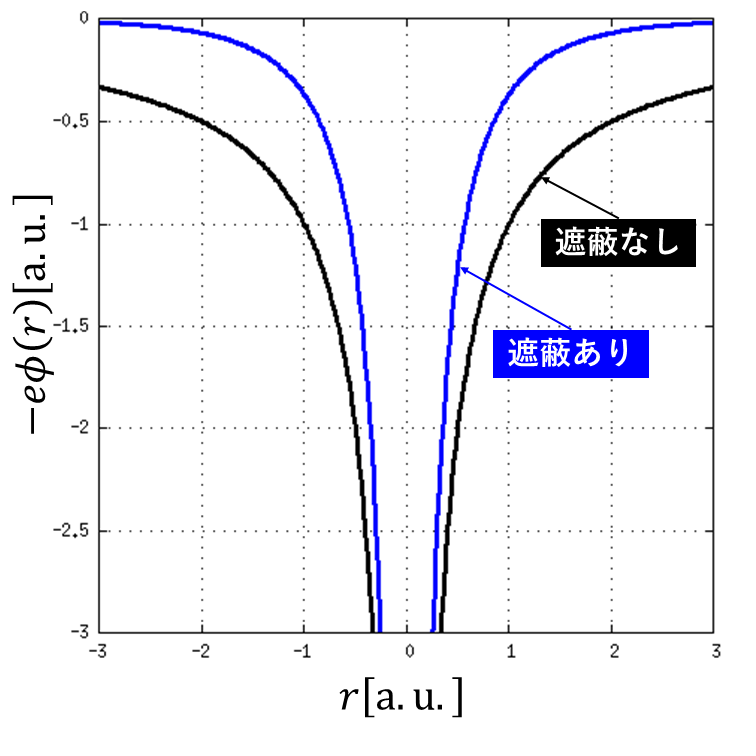
    上図に遮蔽効果を考慮した電子が感じるポテンシャルを示します．遮蔽無しの場合は，\(\frac{1}{r}\) に比例する形になっています．一方，遮蔽ありの場合は \(e^{\frac{r}{\lambda}}\) がかかっているため，減衰がはやくなっています．

イオン化不純物散乱シミュレーション

    不純物をドーピングした半導体では，イオン化不純物散乱ーイオン化した不純物（通常点電荷とみなす）が電子や正孔を散乱する現象ーによる電子移動度の低下が起こります．

    以下に，正のイオン化不純物に電子を発射するシミュレーションを置きました．遮蔽効果がある場合，無い場合で電子の軌道が異なります．遮蔽効果がある場合は，電子の軌道はあまり曲がりません．（=散乱されにくい）このことからわかるように遮蔽が強いほど，電子移動度は大きな値になります．つまり，電流がより流れやすくなります．

    ※以下のシミュレーションで背景の電気力線が明るい時は遮蔽なし，暗い時は遮蔽ありです．