加速定理

加速定理の導出

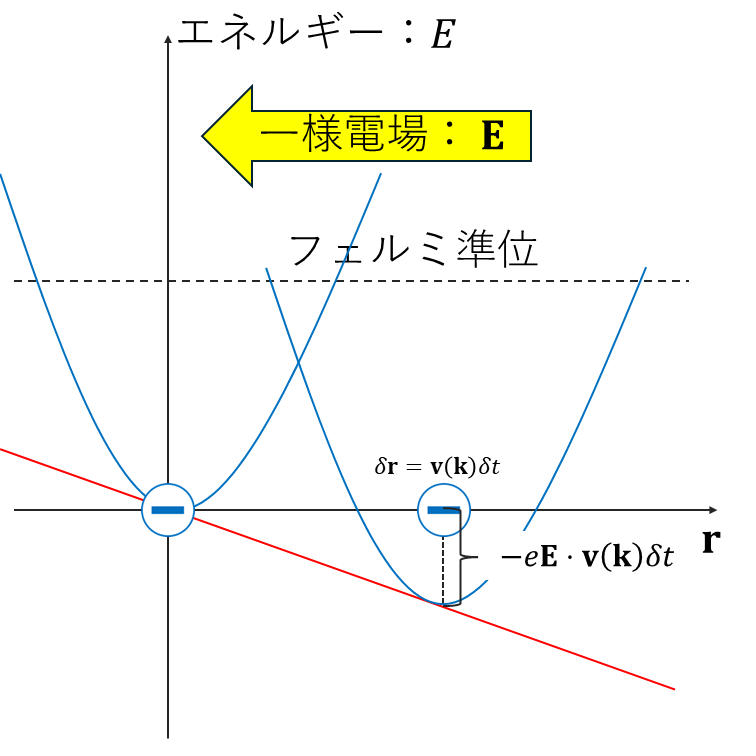
    一様電場 \(\mathbf{E}\) が印加された系を考えます．このとき電子は， \[ \mathbf{F}=-e\mathbf{E} \] だけ電場から力を受けます．時刻が \(t\sim t+\delta t\) だけ発展したとき，電子は \(\mathbf{v}(\mathbf{k})\delta t\) だけ移動します．この間に波数は \(\mathbf{k}\sim \mathbf{k}+\delta \mathbf{k}\)，エネルギーは \(\epsilon(\mathbf{k})\sim\epsilon(\mathbf{k}+\delta \mathbf{k})\) 変化したとしましょう．電子のエネルギーの変化分 \(\delta \epsilon(\mathbf{k}) \) に関して，テイラー展開を用いて計算すると， \[ \begin{split} \delta \epsilon(\mathbf{k})&=\epsilon(\mathbf{k}+\delta\mathbf{k})-\epsilon(\mathbf{k})\\ &=\epsilon(\mathbf{k})+\nabla \epsilon(\mathbf{k})\cdot(\mathbf{k}+\delta\mathbf{k}-\mathbf{k})-\epsilon(\mathbf{k})\\ &=\nabla \epsilon(\mathbf{k})\cdot \delta \mathbf{k} \end{split} \] だけ変化します．上式のテイラー展開は，電子のエネルギーを線形近似していることを意味します．微分可能であれば，エネルギーがどんな関数形でも成り立ちます．ここで，\(\mathbf{v}=\frac{1}{\hbar}\nabla \epsilon(\mathbf{k})\) の関係式を使うと， \[ \begin{split} \delta \epsilon(\mathbf{k})&=\hbar \mathbf{v}(\mathbf{k}) \cdot \delta\mathbf{k} \end{split} \] となります．上のエネルギーの変化分は，上図に示す電磁場からもらった仕事 \(-e\mathbf{E}\cdot \delta \mathbf{r}=-e\mathbf{E}\cdot \mathbf{v}(\mathbf{k})\delta t\) と一致するので， \[ \hbar \mathbf{v}(\mathbf{k}) \cdot \delta\mathbf{k}=-e\mathbf{E}\cdot \mathbf{v}(\mathbf{k})\delta t \] となり，上式より， \[ \frac{d\mathbf{k}}{dt}=-\frac{e}{\hbar}\mathbf{E} \] が成り立ちます．上式は加速定理と呼ばれます．

    たまに，自由電子の場合，\(\mathbf{p}=\hbar\mathbf{k}\) が成り立つので，\(\frac{d\mathbf{p}}{dt}=-e\mathbf{E}\) に代入して上式を導出する方がいらっしゃいます．たしかに同じ式は出てきますが，自由電子に限らず上式は成り立つので注意してください．