鏡像効果 part.1

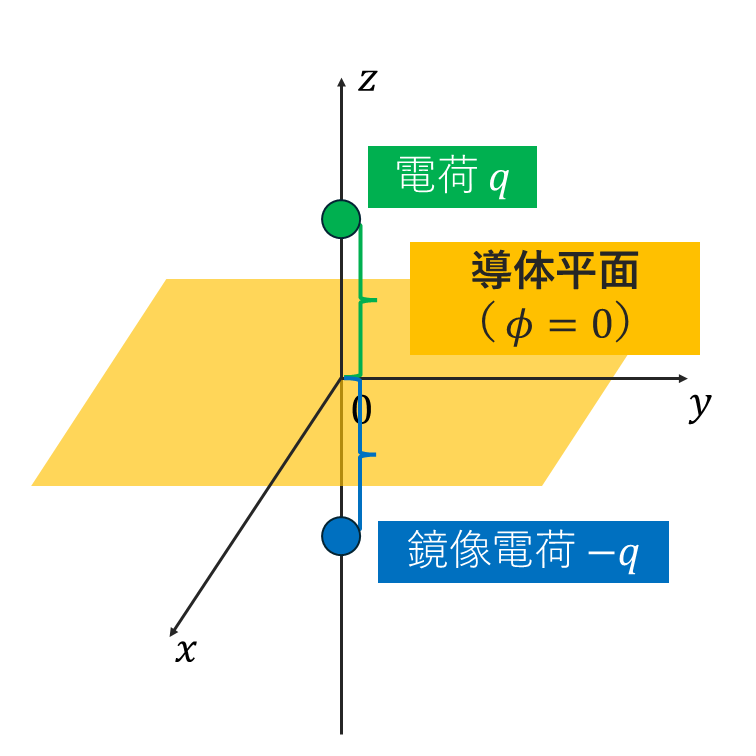
愚直なポテンシャル計算

    上図に示すように，導体平面から \(\frac{l}{2}\) 離れた位置に点電荷 \(q\) があるとします．このとき，点電荷は導体平板に電荷を誘起します．点電荷と誘起された電荷がつくるポテンシャルは，ポアソン方程式： \[\scriptsize \nabla^2\phi(\mathbf{r}_{||},z)=-\frac{1}{\epsilon_0}\left(q\delta(\mathbf{r}_{||})\delta\left(z-\frac{l}{2}\right)+\rho_\mathrm{ind}(\mathbf{r}_{||})\delta(z)\right) \] を解くことにより得られます．ただし，\(r_{||}\) は \((x,y)\)，\(\delta(r_{||})\) や \(\delta(z)\) はデルタ関数，\(\rho_\mathrm{ind}\) は導体平板上の誘起電荷密度です．また，位置座標は \(z>0\) のみ考えます．\(z < 0 \) の場合は系を上下反転させればよいです．\(z=0\) の場合，境界条件 \(\phi=0\) を課しているため，そのまま \(\phi=0\) となります．これは，点電荷が完全に遮蔽されたことを意味しています．実際にはそんなことありえないので，2次元系における遮蔽効果の計算を行う必要があります．（例えば，こちらの記事の方法を2次元系に焼きなおして）

    では，上のポアソン方程式を解いていきましょう．誘起電荷密度は，境界条件を設定することにより自然に求まるため，一旦無視します： \[ \nabla^2\phi(\mathbf{r}_{||},z)=-\frac{q}{\epsilon_0}\delta(\mathbf{r}_{||})\delta\left(z-\frac{l}{2}\right) \] 今考えている系では，円筒対称性があります．そこで，2次元フーリエ変換します： \[\scriptsize \phi(\mathbf{r}_{||},z)=\frac{1}{(2\pi)^2}\int d\mathbf{q}_{||} \Phi(\mathbf{q}_{||},z)e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}}~~~~~~(\mathbf{q}_{||}=(q_x,q_y)) \] \[ \delta(\mathbf{r}_{||})=\frac{1}{(2\pi)^2}\int d\mathbf{q}_{||} e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}} \] より \[\scriptsize \nabla^2\frac{1}{(2\pi)^2}\int d\mathbf{q}_{||} \Phi(\mathbf{q}_{||},z)e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}}=-\frac{q}{\epsilon_0}\frac{1}{(2\pi)^2}\int d\mathbf{q}_{||} e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}}\delta\left(z-\frac{l}{2}\right) \] となり，微分を実行し，両辺のフーリエ成分を比較すると， \[ \left(-q_{||}^2+\frac{d^2}{dz^2}\right) \Phi(\mathbf{q}_{||},z)=-\frac{q}{\epsilon_0}\delta\left(z-\frac{l}{2}\right) \] となります．上の微分方程式は，演算子法を用いて解きます．\(\frac{d}{dz}=D_z\) と置き，式を以下の様に変形します： \[ \left(D_z^2-q_{||}^2\right) \Phi(\mathbf{q}_{||},z)=-\frac{q}{\epsilon_0}\delta\left(z-\frac{l}{2}\right) \] ↓\(\left(D_z^2-q_{||}^2\right)\) の逆演算子を両辺に演算 \[ \Phi(\mathbf{q}_{||},z)=-\frac{q}{\epsilon_0}\frac{1}{D_z+q_{||}}\frac{1}{D_z-q_{||}}\delta\left(z-\frac{l}{2}\right) \] ここで，演算子法の公式： \[ \frac{1}{D-a}f(x)=e^{ax}\int e^{-ax}f(x)dx \] を用いると， \[\scriptsize \begin{split} &\Phi(\mathbf{q}_{||},z)\\ &=-\frac{q}{\epsilon_0}\frac{1}{D_z+q_{||}} e^{q_{||}z}\int e^{-q_{||}z}\delta\left(z-\frac{l}{2}\right)dz\\ &=-\int dq_z\frac{q}{2\pi\epsilon_0}\frac{1}{D_z+q_{||}} e^{q_{||}z}\int e^{-q_{||}z}e^{-iq_z\left(z-\frac{l}{2}\right)}dz~~~~~~(デルタ関数をフーリエ変換)\\ &=-\int dq_z\frac{q}{2\pi\epsilon_0}\frac{1}{D_z+q_{||}} \left[\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{-q_{||}-iq_z}\right]\\ &=-\int dq_z\frac{q}{2\pi\epsilon_0}e^{-q_{||}z}\int e^{q_{||}z}\left[\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{-q_{||}-iq_z} \right]dz\\ &=-\int dq_z\frac{q}{2\pi\epsilon_0}\left[\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{(-q_{||}-iq_z)(q_{||}-iq_z)} \right]\\ &=\int dq_z\frac{q}{2\pi\epsilon_0}\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{q_{||}^2+q_z^2} \end{split} \] となります．微分方程式の解は，上の階に同次形微分方程式： \[ \left(-q_{||}^2+\frac{d^2}{dz^2}\right) \Phi(\mathbf{q}_{||},z)=0 \] の解である \[ \Phi(\mathbf{q}_{||},z)=Ce^{q_{||}z}+De^{-q_{||}z}~~~(C,D は任意定数) \] を足し合わせたものになるため，ポテンシャルのフーリエ成分は， \[ \Phi(\mathbf{q}_{||},z)=Ce^{q_{||}z}+De^{-q_{||}z}+\int dq_z\frac{q}{2\pi\epsilon_0}\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{q_{||}^2+q_z^2} \] となります．ここで，境界条件を課しましょう．まず，\(z\rightarrow \infty\) でポテンシャルが発散しないようにするためには，\(C=0\) である必要があります．また，導体平面上で \(\phi=0\) になる条件を課すと， \[ \Phi(\mathbf{q}_{||},z=0)=D+\int dq_z\frac{q}{2\pi\epsilon_0}\frac{e^{iq_z\frac{l}{2}}}{q_{||}^2+q_z^2}=0 \] より， \[ D=-\int dq_z\frac{q}{2\pi\epsilon_0}\frac{e^{iq_z\frac{l}{2}}}{q_{||}^2+q_z^2} \] が得られます．これより，ポアソン方程式の解は， \[\scriptsize \begin{split} &\phi(\mathbf{r}_{||},z)\\ &=\frac{1}{(2\pi)^2}\int d\mathbf{q}_{||}\int dq_z \left[ \frac{q}{2\pi\epsilon_0}\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{q_{||}^2+q_z^2} -\frac{q}{2\pi\epsilon_0}\frac{e^{-q_{||}z+iq_z\frac{l}{2}}}{q_{||}^2+q_z^2} \right] e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}}\\ &=\frac{1}{(2\pi)^3}\frac{q}{\epsilon_0}\int d\mathbf{q}_{||}\int dq_z \left[ \frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{q_{||}^2+q_z^2} -\frac{e^{-q_{||}z+iq_z\frac{l}{2}}}{q_{||}^2+q_z^2} \right] e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}} \end{split} \] になります．あとは，積分を実行するだけです．順に計算していきましょう．まずは，\(q_z\) に関する積分です．複素積分を利用します．まずは， \[\scriptsize \begin{split} &\int dq_z \left[\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{q_{||}^2+q_z^2} -\frac{e^{-q_{||}z+iq_z\frac{l}{2}}}{q_{||}^2+q_z^2}\right]\\ &=\frac{1}{2q_{||}i}\int_{-\infty}^\infty dq_z \left(\frac{1}{q_z-iq_{||}}-\frac{1}{q_z+iq_{||}}\right)\left(e^{-iq_z\left(z-\frac{l}{2}\right)}-e^{-q_{||}z+iq_z\frac{l}{2}}\right) \end{split} \] と変形します．

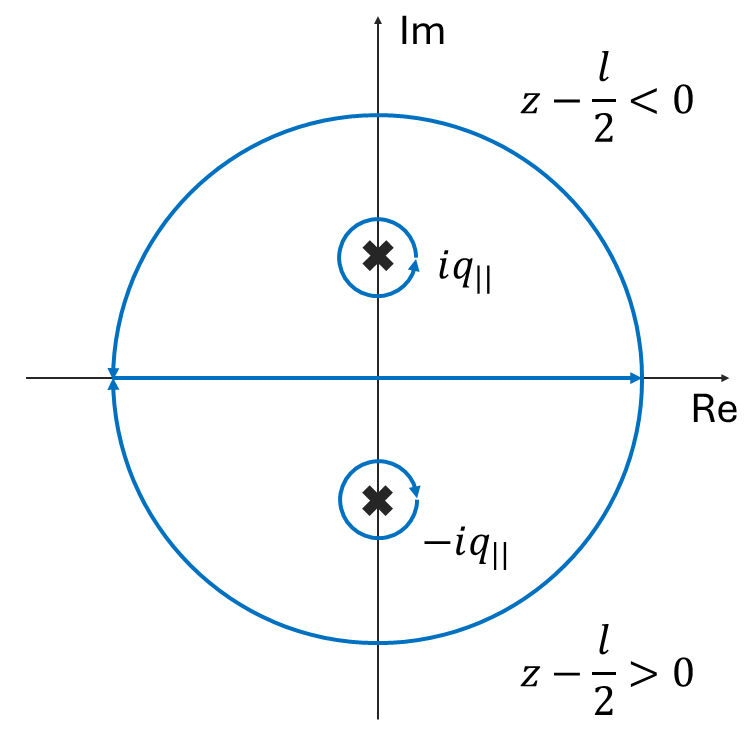
上図に示す，積分経路で積分を実行すると， \[\scriptsize \begin{split} &\int dq_z \left[\frac{e^{-iq_z\left(z-\frac{l}{2}\right)}}{q_{||}^2+q_z^2} -\frac{e^{-q_{||}z+iq_z\frac{l}{2}}}{q_{||}^2+q_z^2}\right]\\ &=\frac{1}{2q_{||}i}2\pi i\left(\mathrm{Res}\left(-iq_{||}\right)\Theta\left(z-\frac{l}{2}\right)+\mathrm{Res}\left(iq_{||}\right)\Theta\left(-z+\frac{l}{2}\right)-\mathrm{Res}\left(iq_{||}\right)e^{-q_{||}z}\right)\\ &=\frac{1}{2q_{||}i}2\pi i\left(e^{-q_{||}\left(z-\frac{l}{2}\right)}\Theta\left(z-\frac{l}{2}\right)+e^{q_{||}\left(z-\frac{l}{2}\right)}\Theta\left(-z+\frac{l}{2}\right)-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)\\ &=\frac{\pi }{q_{||}}\left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)\\ \end{split} \] となります．この結果より， \[ \begin{split} &\phi(\mathbf{r}_{||},z)\\ &=\frac{1}{(2\pi)^3}\frac{q}{\epsilon_0}\int d\mathbf{q}_{||} e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}}\frac{\pi }{q_{||}}\left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)\\ &=\frac{\pi }{(2\pi)^3}\frac{q}{\epsilon_0}\int d\mathbf{q}_{||} e^{-i\mathbf{q}_{||}\cdot\mathbf{r}_{||}}\frac{1}{q_{||}}\left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)\\ \end{split} \] となります．今考えている系には円筒対称性があるため，極座標を用いると，（\(q_{||}\) は \(x\) 方向を向いているとします．円筒対称性があるため，積分結果は同じ．どの方向でも OK） \[\scriptsize \begin{split} &\phi(\mathbf{r}_{||},z)\\ &=\frac{\pi }{(2\pi)^3}\frac{q}{\epsilon_0}\int_0^\infty dq_{||} \int_{0}^{2\pi}d\theta~q_{||} e^{-i{q}_{||}{r}_{||}\cos\theta}\frac{1}{q_{||}}\left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)\\ &=\frac{\pi }{(2\pi)^3}\frac{q}{\epsilon_0}\int_0^\infty dq_{||} \left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)\int_{0}^{2\pi}d\theta~ e^{-i{q}_{||}{r}_{||}\cos\theta} \end{split} \] と書けます．ここで，\(\theta\) 積分の結果は第1種0次ベッセル関数 \(J_0(q_{||},r_{||})\) に \(2\pi\) を乗じたものになるため， \[\scriptsize \begin{split} &\phi(\mathbf{r}_{||},z)\\ &=\frac{\pi }{(2\pi)^3}\frac{q}{\epsilon_0}\int_0^\infty dq_{||} \left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)2\pi J_0(q_{||}r_{||})\\ &=\frac{q}{4\pi \epsilon_0}\int_0^\infty dq_{||} \left(e^{-q_{||}\left|z-\frac{l}{2}\right|}-e^{-q_{||}\left(z+\frac{l}{2}\right)}\right)J_0(q_{||}r_{||}) \end{split} \] となります．上の積分はハンケル変換の形をしており，ハンケル変換の表（リンクは wiki）を参考にすると， \[\scriptsize \begin{split} &\phi(\mathbf{r}_{||},z)&=\frac{q}{4\pi \epsilon_0}\left[\frac{1}{\sqrt{r_{||}^2+\left(z-\frac{l}{2}\right)^2}}-\frac{1}{\sqrt{r_{||}^2+\left(z+\frac{l}{2}\right)^2}}\right] \end{split} \] が得られます．答えはシンプルですが，愚直に解くと道中が非常に大変です．

鏡像法による計算

    W. トムソンの鏡像法による計算を行いましょう．W. トムソンは上記の問題を解く際に，導体平面をとりはずし，反対の電荷をもつ点電荷 \(-q\) （鏡像電荷）が \(z=-\frac{l}{2}\) に存在するとしました．このようにすれば，\(z=0\) において，\(\phi\) はどこでも \(0\) になります．この場合の，ポテンシャルは， \[ \begin{split} &\phi(\mathbf{r}_{||},z)\\ &=\frac{q}{4\pi \epsilon_0}\frac{1}{\sqrt{r_{||}^2+\left(z-\frac{l}{2}\right)^2}}+\frac{-q}{4\pi \epsilon_0}\frac{1}{\sqrt{r_{||}^2+\left(z+\frac{l}{2}\right)^2}}\\ &=\frac{q}{4\pi \epsilon_0}\left[\frac{1}{\sqrt{r_{||}^2+\left(z-\frac{l}{2}\right)^2}}-\frac{1}{\sqrt{r_{||}^2+\left(z+\frac{l}{2}\right)^2}}\right] \end{split} \] となります．非常に簡単にポテンシャルが求まりました．

数値計算結果

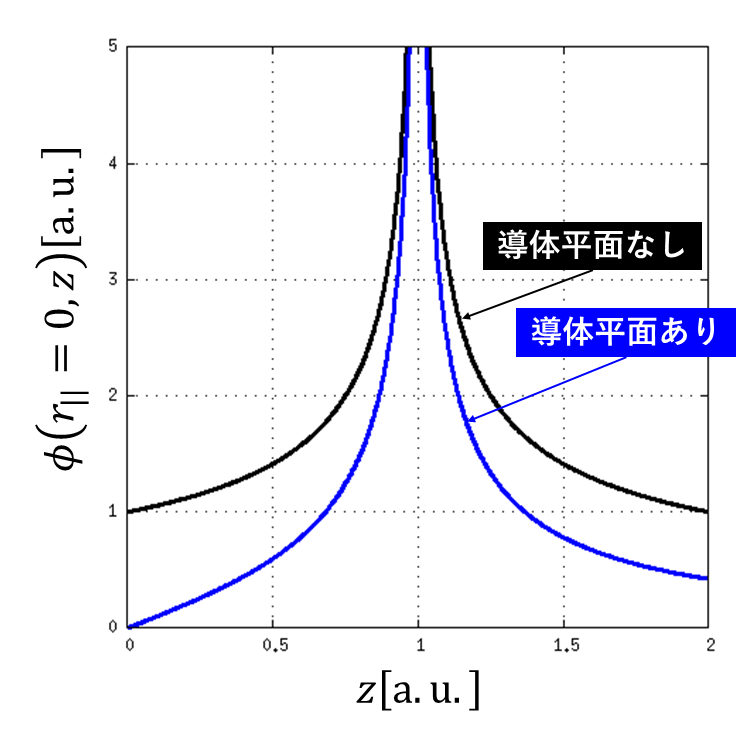
    上図に \(z\) 軸上の電位の数値計算結果を示します．黒線の導体平面無しの場合は，クーロンポテンシャルです．これに対し，青線は導体平面ありの場合で，黒線に比べてポテンシャルが低くなっていることがわかります．これは，導体表面に逆符号の電荷が誘起されたためです．（鏡像電荷は計算手法上でてくる電荷で，本当の電荷ではないので注意．）