電子移動度 part.1

電気抵抗から電子移動度まで

        通常，電流 \(I\) と電圧 \(V\) の関係は，経験式であるオームの法則： \[V=RI\] で与えられます．（これが成り立たない状況も多々あります．頭の隅に置いといてください）上の \(R\) が電流の流れにくさを表す電気抵抗です．上式を電流について解くと， \[I=\frac{1}{R}V=GV\] となります．上の \(G=\frac{1}{R}\) が電流の流れやすさを表すコンダクタンスです．（電圧 \(V\) を印加したときに，どのくらいの電流が流れるかを表します．）

        電気抵抗 \(R\) やコンダクタンス \(G\)は，導体のサイズに依存する値です．例えば，長さ \(L\)，断面積 \(S\) の導体を考えてみましょう．この場合の電気抵抗，コンダクタンスは， \[R=\frac{L}{S}\rho\] \[G=\frac{S}{L}\frac{1}{\rho}=\frac{S}{L}\sigma\] と書けます．上の \(\rho\)，\(\sigma\) はそれぞれ電気抵抗率，電気伝導率です．電気抵抗率も，電気伝導率も導体のサイズには依存しない値です．

    上のコンダクタンスを用いると， \[I=\frac{S}{L}\sigma V\] となります．両辺に，\(\frac{1}{S}\) をかけると， \[\frac{I}{S}=\sigma \frac{V}{L}\] と書けます．上式の左辺は電流密度 \(j\)，右辺の \(\frac{V}{L}\) は電場 \(E\) ですので， \[j=\sigma E\] となります．電場 \(E\) を印加した場合に，どの程度の電流密度になるかを表すのが，電気伝導度 \(\sigma\) です．

    さて，電流密度 \(j\) は， \[ j=env_d \] と書けます．ただし，\(n\) はキャリアの数密度，\(v_d\) はドリフト速度です．この式と電気伝導度の式を結びつけると， \[ env_d=\sigma E \] となり，ドリフト速度について解くと， \[ v_d=\frac{\sigma}{en} E=\mu E \] \[ \mu=\frac{\sigma}{en} \] となります．\(\mu\) は移動度と呼ばれます．キャリアが電子の場合は，電子移動度と呼ばれます．電場 \(E\) が印加されたとき，キャリアの平均速度であるドリフト速度がどの程度の値になるかを表します．移動度は，キャリアの個数に関係ない値です．（これは，\(en\) で割っている個所に関する説明です．厳密には，移動度はフェルミ波数等の電荷密度で決まる値に依存します．）

補足：簡単な電子移動度式の導出

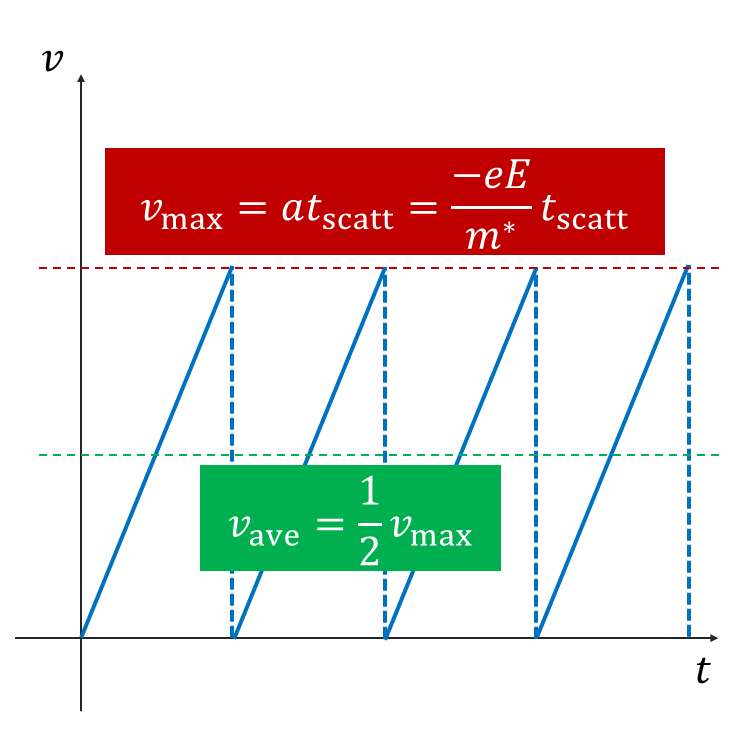
    簡単な電子移動度式の導出をしてみましょう．一次元の系に電場 \(E\) が印加され，電子が加速されたことを考えます．電子は，時刻 \(t_\mathrm{scatt}\) が経過する度に散乱を受け，速度が 0 になるとします（上図）．なお，\(t_\mathrm{scatt}\) は緩和時間といいます．このときの電子のドリフト速度を計算してみましょう．運動方程式は， \[ m^*a=-eE~~~(m^* は有効質量) \] であるので，電子の速度は， \[ v(t)=-\frac{eE}{m^*}t \] と書けます．このとき，電子の平均速度，すなわちドリフト速度は， \[ v_d(t)=-\frac{et_\mathrm{scatt}}{2m^*}E \] となり，電流の方向を気にしなければ，移動度は \(E\) の係数部分であるため， \[ \mu=\frac{et_\mathrm{scatt}}{2m^*} \] となります．電子移動度は，よく \[ \mu=\frac{e\tau}{m^*} \] と書かれます．（\(\tau=t_\mathrm{scatt}\) と考えてください．）この式と2倍差異がありますが，上の簡単なモデルでも移動度の式を出すことができました．

    電子移動度： \[ \mu=\frac{e\tau}{m^*} \] を考察してみましょう．\(e\) は素電荷ですが，電子が電場からどの程度の力を受けるかを決める値になっています．仮に，\(e\) が素電荷より大きな値をとることがあれば，電子移動度は高くなります．\(\tau\) は散乱による効果を表し，\(\tau\) の値が小さいほど頻繁に散乱されることを意味します．ここでは詳細に触れませんが，\(\tau\) は散乱確率の逆数で計算されます．最後に，電子移動度は \(m^*\) に反比例します．\(m^*\) は慣性であり，値が大きいほど電子が動きづらくなります．このため，反比例の形になっています．