電子移動度 part.3

ボルツマン輸送方程式の説明

    ボルツマン輸送方程式は，以下の編微分方程式です： \[\scriptsize \frac{\partial f(\mathbf{r},\mathbf{k},t)}{\partial t} +\mathbf{v}\cdot \nabla_\mathbf{r}f(\mathbf{r},\mathbf{k},t) -\frac{e}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f(\mathbf{r},\mathbf{k},t) =\left(\frac{\partial f(\mathbf{r},\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt} \] 上式の \(f(\mathbf{r},\mathbf{k},t)\) は6次元位相空間の分布関数です．ここでは，電子について考えるので，電子の分布関数になります．\(\mathbf{r}\sim\mathbf{r}+\Delta \mathbf{r}，かつ，\mathbf{k}\sim\mathbf{k}+\Delta \mathbf{k}\) に存在する電子数は \[ \mathrm{（電子数）}=f(\mathbf{r},\mathbf{k},t)D(\mathbf{r},\mathbf{k})\Delta \mathbf{r} \Delta \mathbf{k} \] で表されます．ただし，\(D(\mathbf{r},\mathbf{k})\) は状態密度です．また，\(\mathbf{E}\) は電場です．ボルツマン輸送方程式の左辺第一項は分布関数自体の時間変化ー例えば，ガウス分布関数の分散が時間経過で大きくなっていくような変化ーを表し，定常状態では 0 になります．第二項は，拡散項と呼ばれ，系が一様でない場合に値をもちます．左辺第三項は，外場項と呼ばれ，外聞電場によって電子の波数が変化した場合の分布関数の変化を与えます．最後に，右辺の項は，散乱項と呼ばれます．散乱（古典的には運動量が変化すること，量子論的には量子状態が変化すること）による分布関数の変化を与えます．

系が一様であり定常状態であるとしましょう．また，外部電場は2次の項が無視できる程度に弱いとします．この場合，ボルツマン輸送方程式は， \[ -\frac{e}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f(\mathbf{k}) =\left(\frac{\partial f(\mathbf{k})}{\partial t}\right)_\mathrm{scatt} \] と簡単にできます．ここで，上式を解くために平衡状態からのずれ \[ g(\mathbf{k})=f(\mathbf{k})-f_0(\mathbf{k}) \] を導入します．上式右辺の第二項はフェルミ分布関数です．上式を使うと，ボルツマン輸送方程式は， \[ -\frac{e}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}(g(\mathbf{k})+f_0(\mathbf{k})) =\left(\frac{\partial(g(\mathbf{k})+f_0(\mathbf{k})) }{\partial t}\right)_\mathrm{scatt} \] より， \[ -\frac{e}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k}) =\left(\frac{\partial g(\mathbf{k}) }{\partial t}\right)_\mathrm{scatt} \] となります．ただし，\(\mathbf{E}\cdot \nabla_\mathbf{k}g(\mathbf{k})\) の項は電場の2次のこうであるため無視しました．

緩和時間近似

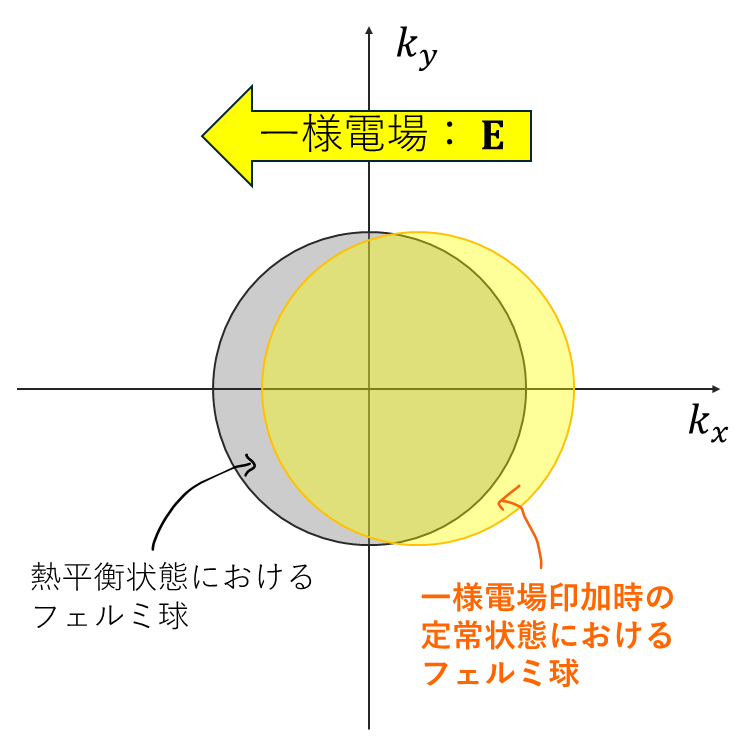
    上でボルツマン輸送方程式を簡単な形に変形してきました．ここでは，緩和時間近似を導入することにより，近似的な解を求めます．緩和時間近似では，ボルツマン輸送方程式の散乱項を， \[ \left(\frac{\partial g(\mathbf{k}) }{\partial t}\right)_\mathrm{scatt} =-\frac{g(\mathbf{k})}{\tau} \] と置きます．これは，\(g(\mathrm{k},t)\propto e^{-\frac{t}{\tau}}\) であることを意味しています．何もしなければ，時刻 \(\tau\) 経過すると熱平衡状態に戻ることを意味しています．上式をボルツマン輸送方程式に用いると， \[ -\frac{e}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k}) =-\frac{g(\mathbf{k})}{\tau} \] より， \[ g(\mathbf{k})=\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k}) \] となり， \[ \begin{split} f(\mathbf{k})&=f_0(\mathbf{k})+\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k})\\ &=f_0\left(\mathbf{k}+\frac{e\tau}{\hbar}\mathbf{E}\right) \end{split} \] が得られます．上式は，上図に示すように，外部電場を印加した場合，平衡状態からフェルミ分布がシフトすることを表します．シフトする方向は，電場と反対の方向です．電場を切ると，時刻 \(\tau\) 経過したとき，元の平衡状態の分布ーフェルミ分布関数ーに戻ります．

電子移動度の導出

    上で分布関数が得られたので，電子の平均速度ーすなわち，ドリフト速度ーを計算して，電子移動度を導出しましょう．ドリフト速度は， \[ \begin{split} \mathbf{v_d}&=\frac{\int \mathbf{v}(\mathbf{k})f(\mathbf{k})D(\mathbf{k})d\mathbf{k}}{\int f(\mathbf{k})D(\mathbf{k})d\mathbf{k}} \end{split} \] で計算されます．上式右辺の分母は電子数 \(N\) を表しています．分子は，波数 \(\mathbf{k}\sim\mathbf{k}+\delta\mathbf{k}\) の電子数 \(dN(\mathbf{k})=f(\mathbf{k})D(\mathbf{k})d\mathbf{k}\) に速度 \(\mathbf{v}(\mathbf{k})\) をかけた形になっています．なお，積分範囲は伝導帯の電子です．式全体としては，伝導に寄与する全電子の平均速度になっています．（故に左辺はドリフト速度）上式の分母を電子数 \(N\) にし，上で得られた緩和時間近似の結果を代入すると， \[ \begin{split} \mathbf{v_d}&=\frac{1}{N}\int \mathbf{v}(\mathbf{k})\left(f_0(\mathbf{k})+\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k})\right)D(\mathbf{k})d\mathbf{k}\\ &=\frac{1}{N}\int \mathbf{v}(\mathbf{k})\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k})D(\mathbf{k})d\mathbf{k}\\ \end{split} \] となります．ただし，\(f_0\) の項は熱平衡状態の平均速度を意味し，積分値は 0 になります．ここで，波数積分からエネルギー積分に変換すると， \[ \begin{split} \mathbf{v_d}&=\frac{1}{N}\int \mathbf{v}(\mathbf{k})\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}\epsilon(\mathrm{k})\frac{\partial}{\partial \epsilon}f_0(\epsilon)D(\epsilon)d\epsilon\\ &=\frac{1}{N}\int \mathbf{v}(\mathbf{k})\frac{e\tau}{\hbar}\mathbf{E}\cdot \hbar\mathbf{v}\frac{\partial}{\partial \epsilon}f_0(\epsilon)D(\epsilon)d\epsilon\\ \end{split} \] と書けます．ただし，\(\nabla \epsilon = \hbar \mathbf{v}\) の関係式を使いました．上式の \(\frac{\partial}{\partial \epsilon}f_0(\epsilon)\) を化学ポテンシャル \(\mu_c\) を使って \(-\frac{\partial}{\partial \mu_c}f_0(\epsilon - \mu_c)\) と書きかえて式を整理すると， \[ \begin{split} \mathbf{v_d}&=\frac{1}{N}\int \mathbf{v}(\mathbf{k})\frac{e\tau}{\hbar}\mathbf{E}\cdot \hbar\mathbf{v}\left(-\frac{\partial}{\partial \mu_c}f_0(\epsilon-\mu_c)\right)D(\epsilon)d\epsilon\\ &=e\tau\frac{\partial }{\partial \mu_c}\left[\frac{1}{N}\int\mathbf{v}\mathbf{E}\cdot\mathbf{v}f_0(\epsilon-\mu_c)D(\epsilon)d\epsilon\right] \end{split} \] となります．ここで，今考えている物質が等方的であり，バンドが球対称である場合を考えましょう．また，電場を \(\mathbf{E}=(E,0,0)\) とします．このとき，上式は \[ \begin{split} v_d&=e\tau\frac{\partial }{\partial \mu_c}\left[\frac{1}{N}\int v_x^2Ef_0(\epsilon-\mu)D(\epsilon)d\epsilon\right]\\ &=e\tau\frac{\partial }{\partial \mu_c}\left[\frac{1}{N}\int v_x^2f_0(\epsilon-\mu)D(\epsilon)d\epsilon\right]E\\ &=e\tau\frac{\partial }{\partial \mu_c}\braket{v_x^2}E \end{split} \] となります．ただし，\(\braket{}\) は平均を意味し，\(\braket{v_x^2}\) は熱平衡状態の \(x\) 方向の速さの 2 乗の平均値を意味します．上式から，電子移動度は， \[ \begin{split} \mu &=e\tau\frac{\partial }{\partial \mu_c}\braket{v_x^2} \end{split} \] であることがわかります．今考えている等方的な系の熱平衡状態では，\(\braket{v_x^2}=\braket{v_y^2}=\braket{v_z^2}=\frac{1}{3}\braket{v^2}\) が成り立つので，上式は \[ \begin{split} \mu&=\frac{e\tau}{3}\frac{\partial }{\partial \mu_c}\braket{v^2} \end{split} \] とも書けます．ここで，系が 0 Kであるとしましょう．このとき，フェルミ分布関数はステップ関数になります．伝導帯の底をエネルギーの基準とすれば， \[ \begin{split} v_d &=\frac{e\tau}{3}\frac{\partial }{\partial \mu_c}\braket{v^2}\\ &=\frac{e\tau}{3}\frac{\partial }{\partial \mu_c}\frac{1}{N}\int_0^{\mu_c} v^2D(\epsilon)d\epsilon \end{split} \] と書けます．\(v=\frac{\hbar k}{m^*}=\frac{\sqrt{2m^*\epsilon}}{m^*}\)，\(D(\epsilon)=\frac{1}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{\epsilon}\) の関係式を使って積分を実行すると， \[ \begin{split} \mu &=\frac{e\tau}{3}\frac{\partial }{\partial \mu}\frac{1}{N}\int_0^{\mu_c} \frac{2m^*\epsilon}{{m^*}^2}\frac{1}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{\epsilon}d\epsilon\\ &=\frac{e\tau}{3m^*}\frac{1}{\pi^2N}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\frac{\partial }{\partial \mu_c}\int_0^\mu \epsilon^\frac{3}{2}d\epsilon\\ &=\frac{e\tau}{3m^*}\frac{1}{\pi^2N}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\frac{\partial }{\partial \mu_c}\frac{2}{5}\mu_c^\frac{5}{2}\\ &=\frac{e\tau}{3m^*}\frac{1}{\pi^2N}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\mu_c^\frac{3}{2} \end{split} \] となります．0 Kにおける全電子数は， \[ \begin{split} N&=\int_0^\mu D(\epsilon)d\epsilon &=\frac{1}{3\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{\frac{3}{2}}\mu_c^\frac{3}{2} \end{split} \] ですので，移動度は， \[ \mu=\frac{e\tau}{m^*} \] となります．驚くべきことに，ドルーデモデルの結果と同じになります．（計算はこちらのほうが圧倒的に大変）

緩和時間 \(\tau\) の計算方法（弾性散乱）

    イオン化不純物散乱等のエネルギーの変化を伴わない弾性散乱を考えた場合の，緩和時間を計算してみましょう．散乱によるスピン反転を考えない場合，散乱項は \[\scriptsize \begin{split} &\left(\frac{\partial f(\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt}\\ &=\int \left[f(\mathbf{k'})(1-f(\mathbf{k}))W(\mathbf{k'},\mathbf{k})-f(\mathbf{k})(1-f(\mathbf{k'}))W(\mathbf{k},\mathbf{k'})\right]D(\mathbf{k'})d\mathbf{k'} \end{split} \] で計算されます．ただし，\(W(\mathbf{k},\mathbf{k'})\) は状態 \(\mathbf{k}\) から \(\mathbf{k'}\) への散乱確率です．上式の被積分関数の第一項は状態 \(\mathbf{k'}\) から \(\mathbf{k}\) へ散乱することによる分布関数の変化を，第二項は状態 \(\mathbf{k}\) から \(\mathbf{k'}\) へ散乱することによる分布関数の変化を表しています．また，散乱が起こるためには，始状態が埋まっており終状態が空いている必要があります．この効果は，それぞれ \(f\) と \(1-f\) により取り入れられています．上式右辺の被積分関数の第二項にマイナス符号が付くのは，散乱により状態 \(\mathbf{k'}\sim\mathbf{k'}+\delta \mathbf{k'}\) の電子数が減るためです．

    定常状態では，分布の形は時間変化しません．この場合，以下の詳細釣り合いの原理を使えます（スピン反転を伴う場合は使えないので注意）： \[ W(\mathbf{k'},\mathbf{k})D(\mathbf{k})= W(\mathbf{k'},\mathbf{k'})D(\mathbf{k'}) \] また，始状態と終状態の状態密度が同じであるとしましょう．すると， \[ W(\mathbf{k'},\mathbf{k})=W(\mathbf{k},\mathbf{k'}) \] が成り立ちます．この式を使うと，散乱項は \[\scriptsize \begin{split} &\left(\frac{\partial f(\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt}\\ &=\int \left[f(\mathbf{k'})-f(\mathbf{k})\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'} \end{split} \] と書けます．上式に，緩和時間近似の結果を適用すると， \[\scriptsize \begin{split} &\left(\frac{\partial f(\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt}\\ &=\int \left[f_0(\mathbf{k'})+\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k'})-f_0(\mathbf{k})-\frac{e\tau}{\hbar}\mathbf{E}\cdot \nabla_\mathbf{k}f_0(\mathbf{k})\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ &=\frac{e\tau}{\hbar}\mathbf{E}\cdot \int \left[\nabla_\mathbf{k}f_0(\mathbf{k'})-\nabla_\mathbf{k}f_0(\mathbf{k})\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'} \end{split} \] となり，波数微分をエネルギー微分に変換すると， \[\scriptsize \begin{split} &\left(\frac{\partial f(\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt}\\ &=\frac{e\tau}{\hbar}\mathbf{E}\cdot \int \left[\hbar \mathbf{v}(\mathbf{k'})\frac{\partial}{\partial \epsilon}f_0(\epsilon')-\hbar \mathbf{v}(\mathbf{k})\frac{\partial}{\partial \epsilon}f_0(\epsilon)\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ &=e\tau\mathbf{E}\cdot \int \left[\mathbf{v}(\mathbf{k'})\frac{\partial}{\partial \epsilon}f_0(\epsilon')-\mathbf{v}(\mathbf{k})\frac{\partial}{\partial \epsilon}f_0(\epsilon)\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ \end{split} \] となります．弾性散乱の場合，\(\epsilon=\epsilon'\) ですので，\(\frac{\partial f_0(\epsilon')}{\partial \epsilon}=\frac{\partial f_0(\epsilon)}{\partial \epsilon}\) がなりたち， \[\scriptsize \begin{split} &\left(\frac{\partial f(\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt}=e\tau\frac{\partial}{\partial \epsilon}f_0(\epsilon)\mathbf{E}\cdot \int \left[\mathbf{v}(\mathbf{k'})-\mathbf{v}(\mathbf{k})\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ \end{split} \] と書けます．ここで，2. 緩和時間近似の結果である\(\left(\frac{\partial f(\mathbf{k},t)}{\partial t}\right)_\mathrm{scatt}=-\frac{g}{\tau}=-\frac{e}{\hbar}\mathbf{E}\cdot\nabla_\mathbf{k}f_0(\mathbf{k})\) を用いると， \[ \begin{split} &-\frac{e}{\hbar}\mathbf{E}\cdot\nabla_\mathbf{k}f_0(\mathbf{k})\\ &=e\tau\frac{\partial}{\partial \epsilon}f_0(\epsilon)\mathbf{E}\cdot \int \left[\mathbf{v}(\mathbf{k'})-\mathbf{v}(\mathbf{k})\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ \end{split} \] が成り立ちます．上式左辺を \(-e\mathbf{E}\cdot\mathbf{v}(\mathbf{k})\frac{\partial f_0(\epsilon)}{\partial \epsilon}\) と変形し，緩和時間 \(\tau\) について解くと， \[ \begin{split} &\frac{1}{\tau}=\int \left[1-\frac{\mathbf{v}(\mathbf{k'})\cdot \mathbf{E}}{\mathbf{v}(\mathbf{k})\cdot \mathbf{E}}\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ \end{split} \] が得られます．

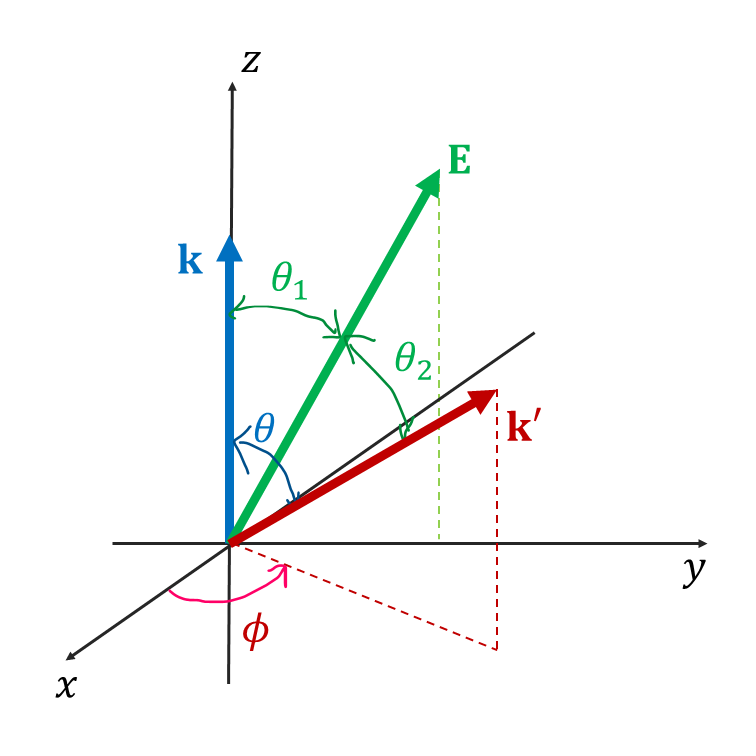
    最後に，\(\frac{\mathbf{v}(\mathbf{k'})\cdot \mathbf{E}}{\mathbf{v}(\mathbf{k})\cdot \mathbf{E}}\) を計算しましょう．電場および速度が上図の様になっているとします．（等方的な系では，上図のものを考えれば OK）このとき， \[ \begin{split} &\frac{1}{\tau}=\int \left[1-\frac{vE\cos\theta_2}{vE\cos\theta_1}\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ &=\int \left[1-\frac{\cos\theta_2}{\cos\theta_1}\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'} \end{split} \] となります．また，上図から各ベクトル方向の単位ベクトルが \[ \mathbf{e}_{\mathbf{k}}= \begin{pmatrix} 0\\0\\1 \end{pmatrix} \] \[ \mathbf{e}_{\mathbf{k'}}= \begin{pmatrix} \sin\theta\cos\phi \\ \sin\theta\sin\phi \\ \cos\theta \end{pmatrix} \] \[ \mathbf{e}_{\mathbf{E}}= \begin{pmatrix} 0 \\ \sin\theta_1 \\ \cos\theta_1 \end{pmatrix} \] と書けることがわかります．\(\mathbf{e}_{\mathbf{k'}}\) と \(\mathbf{e}_{\mathbf{E}}\) の内積を計算すると \[ \mathbf{e}_{\mathbf{k'}}\cdot\mathbf{e}_{\mathbf{E}}=\cos\theta_2=\sin\theta\sin\phi\sin\theta_1+\cos\theta\cos\theta_1 \] の関係式が得られます．これより， \[\scriptsize \begin{split} \frac{1}{\tau} &=\int \left[1-\frac{\sin\theta\sin\phi\sin\theta_1+\cos\theta\cos\theta_1}{\cos\theta_1}\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ &=\int \left[1-\cos\theta\right]W(\mathbf{k},\mathbf{k'})D(\mathbf{k'})d\mathbf{k'}\\ &=\int \left(1-\cos\theta\right)W(\mathbf{k},\mathbf{k'})\frac{d\mathbf{k'}}{(2\pi)^3} \end{split} \] が得られます．ただし，\(\sin\theta\) の積分は奇関数であるため 0 になります．上式は，電子移動度の緩和時間 \(\tau\) を計算するために頻繁に使われます．\(1-\cos\theta\) は，散乱確率のおもみづけであり，前方散乱（散乱角 \(\theta\) が \(0\) に近い）の場合は値が小さく，後方散乱の場合（散乱角 \(\theta\) が \(\pi\) に近い）は値が大きくなります．これは，電流に対する寄与（電子の流れを阻害する影響度）が後方散乱のほうが大きいためです．