内容
ドルーデモデルで電気伝導度と電子移動度の式を導出します.
電気伝導度と電子移動度の導出
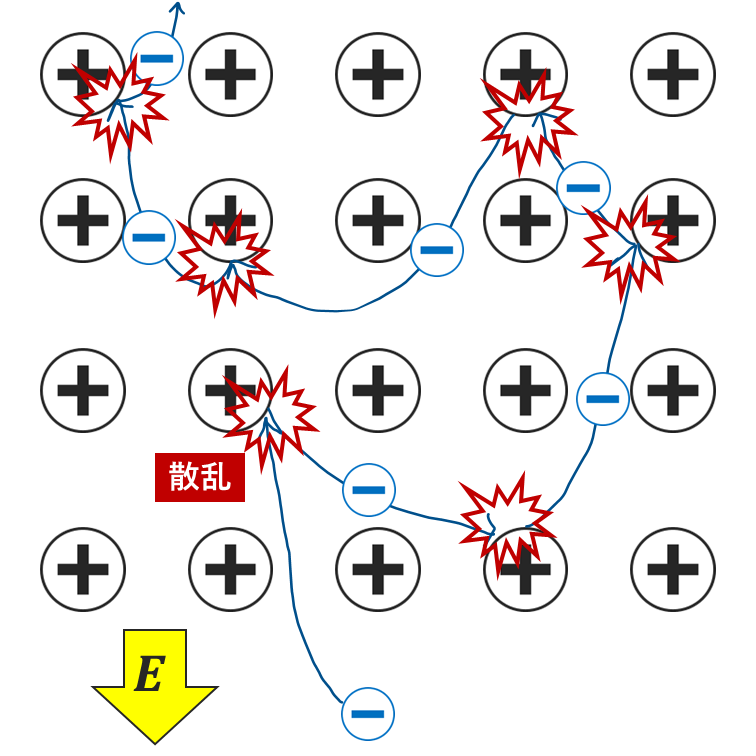
ドルーデモデルについて説明します.ドルーデモデルでは,電子が(1)電場によって加速され,(2)格子(金属や半導体を構成する原子)に散乱(運動量が変わること)されることを考えます(上図).電気伝導度と電子移動度は,(1)の加速と(2)の散乱(減速)がつりあった定常状態の電流密度を計算することにより導出します.
1つの電子が満たす運動方程式を \[ m^*\frac{d \mathbf{v}}{dt} = -e\mathbf{E}-m^*\frac{\mathbf{v}}{\tau} \] と書きます.ただし,\(m^*\) は有効質量,\(\tau\) は緩和時間(散乱と散乱の間の平均時間)です.上式右辺の第二項は,散乱項になっています.\(\frac{m^*\mathbf{v}}{\tau}\) は,緩和時間 \(\tau\) だけ時間が経過すると運動量 \(m^*\tau\) だけ運動量が減少することを意味しています.定常状態を考えると,上式左辺は 0 になります: \[ -e\mathbf{E}-m^*\frac{\mathbf{v_d}}{\tau}=0 \] ここで,速度をドリフト速度に書き換えました.ドリフト速度について解くと, \[ \mathbf{v_d}=-\frac{e\tau}{m^*}\mathbf{E} \] が得られます.電場 \(\mathbf{E}\) の係数は電子移動度に相当します: \[ \mu=\frac{e\tau}{m^*} \] また,電気伝導度は,関連記事を参考にすると, \[ \sigma=ne\mu=\frac{ne^2\tau}{m^*} \] となります.よく見かける数式を導出することができました.数式の意味は関連記事を参考にしてください.
補足:ドルーデモデルで説明できないこと
電場によって加速された電子が,格子に散乱されながら進んでいく(という直感に合う)ことを考えているドルーデモデルですが,説明できないことがいくつかあります.例えば,金属・半導体・絶縁体の伝導特性の違いを説明できません.(=なぜ,金属では電流が流れるのに,絶縁体では流れないのか?を説明できない.)また,"格子に散乱される"という仮定が実はよろしくないです.格子間隔のオーダーで散乱されると考えると,移動度は実験で得られるものに比べてずっと小さな値になっています.結論を言いますと,電子は結晶の周期性の乱れによって散乱されます.格子そのものに散乱されるわけではないのです.
さらなる補足:量子論的に,散乱は「状態が変化すること」です.結晶中では,ブロッホ状態という状態にありますが,周期性が乱れると別の状態になってしまいます.摂動論の言葉で言えば,他の状態に遷移します.