乱雑位相近似

3次元系における乱雑位相近似による遮蔽されたポテンシャルの導出

    3次元で自由電子ガスが存在する空間ー例えば，金属や半導体のバルクーについて考えます．以下では，この空間に正の点電荷 \(q\) を置いた時にできるポテンシャルを計算します．ただし，正の点電荷は \(\mathbf{r}=(0,0,0)\) にあるとします．また，熱平衡状態にあるとします．

    今考えている系で電場をつくる電荷は，正の点電荷 \(q\) と正の点電荷の電場を打ち消すように誘起された電荷です．この場合のポアソン方程式は， \[\nabla^2 \phi(r)=-\frac{1}{\epsilon}\left(q\delta(r)+\rho_\mathrm{ind}(r)\right)\] です．ここで，\(\phi(r)\) は遮蔽効果を考慮したポテンシャル，\(\epsilon\) は物質中の誘電率, \(\rho_\mathrm{ind}\) は正の点電荷によって誘起された電荷の密度（正の点電荷に引き寄せられた電子）です．また，系に球対称性があるため，変数の位置座標 \(\mathbf{r}\) を原点からの距離 \(r\) で書いています．

    上式の \(\rho_\mathrm{ind}\) を一次摂動（量子論）の範囲で計算するのが乱雑位相近似による遮蔽効果の計算です．これから \(\rho_\mathrm{ind}\) を計算するために使用する数式を以下に示します．

・摂動がある場合の電子波動関数 \[ \psi(k,\mathbf{r},t)=\psi_0(k,\mathbf{r},t)+\sum_{k'}C(k',t)\psi_0(k,\mathbf{r},t) \] ・一次摂動の展開係数 \[\scriptsize C(k',t)=-\frac{i}{\hbar}\int_{-\infty}^t \int d\mathbf{r}~\psi_0^*(k',\mathbf{r},t')V(\mathbf{r},t')\psi_0(k,\mathbf{r},t')dt' \] ・無摂動時の分散関係（m^*: 有効質量） \[ E_0(k)=\frac{\hbar^2 k^2}{2m^*} \] ・無摂動時の固有状態（V: 系の体積，系は立方体とし，一辺の長さを L として \(V=L\times L\times L\)） \[ \psi_0(k,\mathbf{r},t)=\frac{1}{\sqrt{V}}\exp \left(i\mathbf{k}\cdot\mathbf{r}-i\frac{E_0(k)}{\hbar} t\right) \] ・摂動ポテンシャル（まずは，一般的な式を使う．） \[ V(\mathbf{r},t)=-e\phi(\mathbf{r},t)=\int V(\mathbf{q},\omega)e^{i\mathbf{q}\cdot\mathbf{r}-i\omega t} d\mathbf{q} d\omega \]

    では，計算を始めていきます．まず，一次摂動の展開係数の計算を進めていきます： \[\scriptsize \begin{split} &C(k',t)\\ &=-\frac{i}{\hbar}\int_{-\infty}^t\int d\mathbf{r}~ \psi_0^*(k',\mathbf{r},t')V(\mathbf{r},t')\psi_0(k,\mathbf{r},t')dt'\\ &=-\frac{i}{\hbar}\int_{-\infty}^t \int d\mathbf{r}~\frac{1}{\sqrt{V}}\exp \left(-i\mathbf{k'}\cdot\mathbf{r}+i\frac{E_0(k')}{\hbar} t'\right)\times\\ &~~~~~~~V(\mathbf{r},t')\frac{1}{\sqrt{V}}\exp \left(i\mathbf{k}\cdot\mathbf{r}-i\frac{E_0(k)}{\hbar} t'\right)dt'\\ &=-\frac{i}{\hbar V}\int_{-\infty}^t\int d\mathbf{r}~ V(\mathbf{r},t')\exp \left(i\left(\mathbf{k}-\mathbf{k'}\right)\cdot\mathbf{r}-i\frac{E_0(k)-E_0(k')}{\hbar} t'\right)dt'\\ \end{split} \] ここで，摂動ポテンシャルの1成分 \(V(\mathbf{r},t)=V(\mathbf{q},\omega)e^{i\mathbf{q,\omega}\cdot\mathbf{r}-i\omega t} \) を代入します（後で和をとります）： \[\scriptsize \begin{split} &C(k',t)\\ &=-\frac{i}{\hbar V}\int_{-\infty}^t dt'\int d\mathbf{r} ~ V(\mathbf{q},\omega)e^{i\mathbf{q}\cdot\mathbf{r}-i\omega t'}e^{i\left(\mathbf{k}-\mathbf{k'}\right)\cdot\mathbf{r}-i\frac{E_0(k)-E_0(k')}{\hbar} t'}\\ &=-\frac{i}{\hbar V}V(\mathbf{q},\omega)\int_{-\infty}^t dt' ~ e^{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} + \omega\right) t'}\int d\mathbf{r}e^{i\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\cdot\mathbf{r}}\\ &=-\frac{i}{\hbar V}V(\mathbf{q},\omega)\int_{-\infty}^t dt' ~ e^{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} + \omega\right) t'}(2\pi)^3\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right) \end{split} \] 時間積分は，収束因子 \(\alpha\) を導入して計算します： \[\scriptsize \begin{split} &C(k',t)\\ &=-\frac{(2\pi)^3i}{\hbar V}V(\mathbf{q},\omega)\int_{-\infty}^t dt' ~ e^{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} +\omega\right) t'+\alpha t'}\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\\ &=-\frac{(2\pi)^3i}{\hbar V}V(\mathbf{q},\omega)\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\frac{e^{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} +\omega\right) t+\alpha t}}{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} +\omega\right) +\alpha }\\ &=\frac{(2\pi)^3}{V}V(\mathbf{q},\omega)\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\frac{e^{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} +\omega\right) t+\alpha t}}{E_0(k)-E_0(k') +\hbar\omega +i\hbar\alpha } \end{split} \] 一次摂動の展開係数が得られました．次は，電子確率密度を計算します．（その後，電子確率密度の和を計算し，無摂動の場合との差を計算すると誘起電子密度が得られます．少しだけ計算が大変ですが，頑張っていきましょう！）

    電子確率密度を計算していきます： \[\scriptsize \begin{split} &\left|\psi(k,\mathbf{r},t)\right|^2\\ &=\left|\psi_0(k,\mathbf{r},t)+\sum_{k'}C(k',t)\psi_0(k,\mathbf{r},t)\right|^2\\ &=\left|\psi_0(k,\mathbf{r},t)\right|^2+\sum_{k',k''}C(k',t)\psi_0(k',\mathbf{r},t)C^*(k'',t)\psi_0^*(k'',\mathbf{r},t)\\ &~~~~+\psi_0^*(k,\mathbf{r},t)\sum_{k'}C(k',t)\psi_0(k',\mathbf{r},t)+c.c. \end{split} \] 上の \(c.c.\) は前の項の複素共役（complex conjugate）です．二次の項は無視します： \[\scriptsize \begin{split} &\left|\psi(k,\mathbf{r},t)\right|^2\\ &=\left|\psi_0(k,\mathbf{r},t)\right|^2+\psi_0^*(k,\mathbf{r},t)\sum_{k'}C(k',t)\psi_0(k',\mathbf{r},t)+c.c.\\ &=\frac{1}{V} + \frac{(2\pi)^3}{V^2}\sum_{k'}V(\mathbf{q},\omega)\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\times\\ &~~~~~~~~~~~~~~~~~~~~~\frac{e^{-i\left(\frac{E_0(k)-E_0(k')}{\hbar} +\omega\right) t+\alpha t}}{E_0(k)-E_0(k') +\hbar\omega +i\hbar\alpha }e^{-i(\mathbf{k}-\mathbf{k'})\cdot \mathbf{r} + i\frac{E_0(k)-E_0(k')}{\hbar} t}+c.c.\\ &=\frac{1}{V} + \frac{(2\pi)^3}{V^2}\sum_{k'}V(\mathbf{q},\omega)\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\times\\ &~~~~~~~~~~~~~~~~~~~~~\frac{e^{i(\mathbf{k'}-\mathbf{k})\cdot \mathbf{r}-i\omega t+\alpha t}}{E_0(k)-E_0(k') +\hbar\omega +i\hbar\alpha }+c.c. \end{split} \] \(k'\) に関する和を積分に直して計算を続けます： \[\scriptsize \begin{split} &\left|\psi(k,\mathbf{r},t)\right|^2\\ &=\frac{1}{V} + \frac{1}{V}\int d\mathbf{k'} V(\mathbf{q},\omega)\delta\left(\mathbf{k}-\mathbf{k'}+\mathbf{q}\right)\frac{e^{i(\mathbf{k'}-\mathbf{k})\cdot \mathbf{r}-i\omega t+\alpha t}}{E_0(k)-E_0(k') +\hbar\omega +i\hbar\alpha }+c.c.\\ &=\frac{1}{V} + \frac{1}{V} V(\mathbf{q},\omega)\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t+\alpha t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega +i\hbar\alpha }+c.c. \end{split} \] 上式から，無摂動の場合の確率密度（第一項）を引くと，確率密度の変化分 \(\delta \rho_{\mathbf{q},\omega}\) が得られます．ついでに，収束因子 \(\alpha=0\)にすると以下のようになります（c.c. の部分もしっかり書きます）： \[ \begin{split} &\delta \rho_{\mathbf{q},\omega}\\ &=\frac{1}{V} V(\mathbf{q},\omega)\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega}\\ &+\frac{1}{V} V^*(\mathbf{q},\omega)\frac{e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega} \end{split} \] 上式は，\(\mathbf{k}\rightarrow \mathbf{k}+\mathbf{q}\) の遷移が発生した結果現れた確率密度の変化分です．

    これまでは，あるポテンシャルのあるフーリエ成分 \(V(\mathbf{r},t)=V(\mathbf{q},\omega)e^{i\mathbf{q}\cdot\mathbf{r}-i\omega t}\) に対して計算してきました．ここで，イオン化不純物等の半導体中の点電荷について考えましょう．これらのポテンシャルは実数で表されるため，\(V(\mathbf{q},\omega)=V^*(\mathbf{q},\omega)=V(-\mathbf{q},-\omega)\) となります．そこで，摂動ポテンシャルを， \[ V(\mathbf{r},t)=V(\mathbf{q},\omega)e^{i\mathbf{q}\cdot\mathbf{r}-i\omega t} + V(\mathbf{q},\omega)e^{-i\mathbf{q}\cdot\mathbf{r}+i\omega t} \] と置き換えます．（最後に \(\mathbf{q}\) に関する和をとるとき，この変更の効果を取り入れます）また，\(\mathbf{k}\rightarrow \mathbf{k}\pm \mathbf{q}\) の遷移が起こるためには，\(\mathbf{k}\) の電子が存在し，\(\mathbf{k}\pm\mathbf{q}\) の状態が空になっている必要があります．このことは，フェルミ分布関数 \(f(E)\) を用いて取り入れます．以上の議論より，電子確率密度の変化分は，以下のように書けます．： \[\scriptsize \begin{split} &\delta \rho_{\mathbf{q},\omega}\\ &=\frac{1}{V} V(\mathbf{q},\omega)\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega}f(E_0(k))(1-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|)))\\ &~~~~+\frac{1}{V} V(\mathbf{q},\omega)\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}-\mathbf{q}\right|) -\hbar\omega}f(E_0(k))(1-f(E_0(\left|\mathbf{k}-\mathbf{q}\right|))) \end{split} \] 誘起電荷密度 \(\rho_\mathrm{ind}\) は，上の電子確率密度の変化分をある状況で存在する自由電子について和をとったものになります．途中，少しトリッキーなことをしますが，順に計算していきます． \[\scriptsize \begin{split} &\rho_\mathrm{ind}\\ &=-e\sum_{\mathbf{k}}\delta \rho_{\mathbf{q},\omega}\\ &=-\frac{e}{V}V(\mathbf{q},\omega)\sum_{\mathbf{k}}\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega}f(E_0(k))(1-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|)))\\ &-\frac{e}{V}V(\mathbf{q},\omega)\sum_{\mathbf{k}}\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}-\mathbf{q}\right|) -\hbar\omega}f(E_0(k))(1-f(E_0(\left|\mathbf{k}-\mathbf{q}\right|)))\\ &=-\frac{e}{V}V(\mathbf{q},\omega)\sum_{\mathbf{k}}\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega}f(E_0(k))(1-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|)))\\ &-\frac{e}{V}V(\mathbf{q},\omega)\sum_{\mathbf{k'}=\mathbf{k}-\mathbf{q}}\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(\left|\mathbf{k'}+\mathbf{q}\right|)-E_0(k') -\hbar\omega}\times\\ &~~~~~~~~~~~~~~~~~~~~~~~f(E_0(\left|\mathbf{k'}+\mathbf{q}\right|))(1-f(E_0(k')))\\ \end{split} \] \(\mathbf{k}\) に関する和と，\(\mathbf{k'}\) に関する和は，どちらも全波数空間に渡る和なので同じです．このことを考慮すると： \[\scriptsize \begin{split} &\rho_\mathrm{ind}\\ &=-\frac{e}{V}V(\mathbf{q},\omega)\times\\ &\sum_{\mathbf{k}}\left[\frac{e^{i\mathbf{q}\cdot \mathbf{r}-i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}+i\omega t}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|) +\hbar\omega}f(E_0(k))(1-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|)))\right.\\ &\left.+\frac{e^{i\mathbf{q}\cdot \mathbf{r}+i\omega t}+e^{-i\mathbf{q}\cdot \mathbf{r}-i\omega t}}{E_0(\left|\mathbf{k'}+\mathbf{q}\right|)-E_0(k') -\hbar\omega}f(E_0(\left|\mathbf{k'}+\mathbf{q}\right|))(1-f(E_0(k')))\right]\\ \end{split} \] と書けます．ポテンシャルが時間変化する場合は，上式が誘起電子密度になります．（時間依存する場合の数式を出したくて，ここまでわざわざ計算してきました...）今回は，時間に依存しない場合を考えます．したがって，\(\omega=0\) となり， \[\scriptsize \begin{split} &\rho_\mathrm{ind}\\ &=-\frac{e}{V}V(\mathbf{q})\sum_{\mathbf{k}}\left[\frac{e^{i\mathbf{q}\cdot \mathbf{r}}+e^{-i\mathbf{q}\cdot \mathbf{r}}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}f(E_0(k))(1-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|)))\right.\\ &\left.+\frac{e^{i\mathbf{q}\cdot \mathbf{r}}+e^{-i\mathbf{q}\cdot \mathbf{r}}}{E_0(\left|\mathbf{k'}+\mathbf{q}\right|)-E_0(k')}f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))(1-f(E_0(k)))\right]\\ &=-\frac{e}{V}V(\mathbf{q})\sum_{\mathbf{k}}\frac{e^{i\mathbf{q}\cdot \mathbf{r}}+e^{-i\mathbf{q}\cdot \mathbf{r}}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}\times\\ &~~~~~\left[f(E_0(k))(1-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|)))-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))(1-f(E_0(k)))\right]\\ &=-\frac{e}{V}V(\mathbf{q})\sum_{\mathbf{k}}\frac{e^{i\mathbf{q}\cdot \mathbf{r}}+e^{-i\mathbf{q}\cdot \mathbf{r}}}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}\left[f(E_0(k))-f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))\right]\\ &=\frac{e}{V}V(\mathbf{q})(e^{i\mathbf{q}\cdot \mathbf{r}}+e^{-i\mathbf{q}\cdot \mathbf{r}})\sum_{\mathbf{k}}\frac{f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))-f(E_0(k))}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}\\ \end{split} \] が得られます．

    誘起電子密度が得られたので，もともとのポアソン方程式に戻りましょう．元々のポアソン方程式は， \[\nabla^2 \phi(r)=-\frac{1}{\epsilon}\left(q\delta(r)+\rho_\mathrm{ind}(r)\right)\] でした．一方，上で求めた誘起電子密度は，摂動ポテンシャル \(V(\mathbf{q})e^{i\mathbf{q}\cdot\mathbf{r}} + V(\mathbf{q})e^{-i\mathbf{q}\cdot\mathbf{r}}\) に対するものでした．ここをリンクさせるためには，上式をフーリエ変換した形に直す必要があります．関連記事を参考にして，上式をフーリエ変換の形に直すと， \[\scriptsize -k^2 \phi(k)(e^{i\mathbf{k}\cdot\mathbf{r}}+e^{-i\mathbf{k}\cdot\mathbf{r}})=-\frac{1}{\epsilon}\left(q(e^{i\mathbf{k}\cdot\mathbf{r}}+e^{-i\mathrm{k}\cdot\mathbf{r}})+\rho_\mathrm{ind}(q)\right)\] となります．ここに上で得られた誘起電子密度を代入すると，（\(V(\mathbf{q})\)）を\(-e\phi(\mathbf{q})\) になおします） \[\scriptsize \begin{split} &-k^2 \phi(k)(e^{i\mathbf{k}\cdot\mathbf{r}}+e^{-i\mathrm{k}\cdot\mathbf{r}})\\ &=-\frac{1}{\epsilon}\left(q(e^{i\mathbf{k}\cdot\mathbf{r}}+e^{-i\mathbf{k}\cdot\mathbf{r}})\right.\\ &\left.-\frac{e^2}{V}\phi(k)(e^{i\mathbf{k}\cdot \mathbf{r}}+e^{-i\mathbf{k}\cdot \mathbf{r}})\sum_{\mathbf{k'}}\frac{f(E_0(\left|\mathbf{k'}+\mathbf{k}\right|))-f(E_0(k'))}{E_0(k')-E_0(\left|\mathbf{k'}+\mathbf{k}\right|)}\right) \end{split} \] となり，式を整理すると \[\scriptsize \phi(k)=\frac{q}{\epsilon k^2}\frac{1}{1+\frac{1}{V}\frac{e^2}{\epsilon k^2}\sum_{\mathbf{k'}}\frac{f(E_0(\left|\mathbf{k'}+\mathbf{k}\right|))-f(E_0(k'))}{E_0(k')-E_0(\left|\mathbf{k'}+\mathbf{k}\right|)}}\] が得られます．上式右辺の分母はリンドハード誘電関数と呼ばれます（\(k\rightarrow q, k'\rightarrow k\) と書きなおします．いろいろ紛らわしくてごめんなさい...）： \[\epsilon(\mathrm{q})=1+\frac{1}{V}\frac{e^2}{\epsilon q^2}\sum_{\mathbf{k}}\frac{f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))-f(E_0(k))}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}\] 点電荷の場合は，全波数同じ重みで \(\phi(k)\) を足し合わせればよいです．したがって，実空間のポテンシャルは，以下のように書けます．： \[\phi(r)=\frac{1}{(2\pi)^3}\int d\mathbf{q}\frac{q}{\epsilon k^2 \epsilon(\mathrm{q})}\] ※ここから先は数値計算の必要があります．

数式の解説

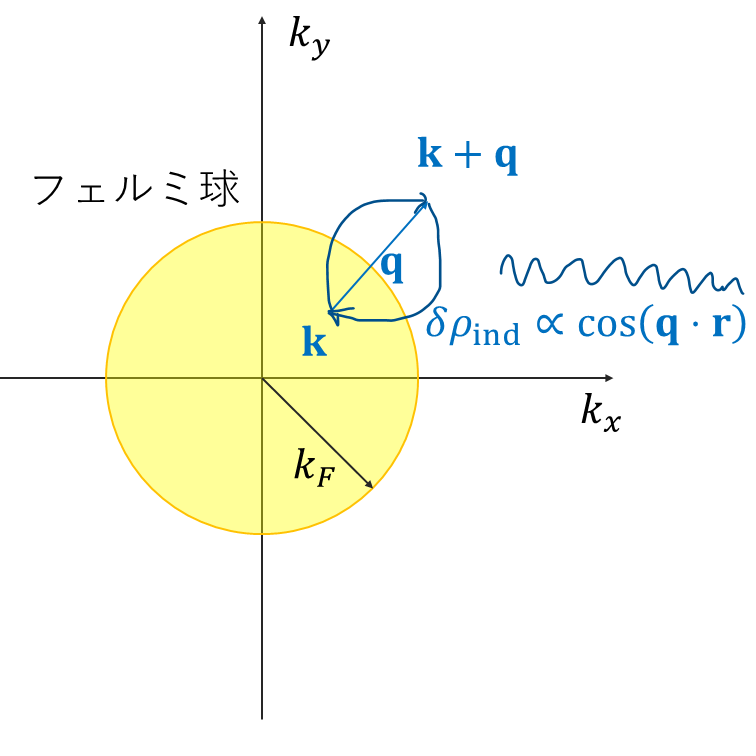
    今回得られた結果を，関連記事のトーマス・フェルミ近似の誘電関数と比較してみましょう．： \[ \begin{split} &\epsilon(\mathrm{q})=1+\frac{1}{V}\frac{e^2}{\epsilon q^2}\sum_{\mathbf{k}}\frac{f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))-f(E_0(k))}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}\\ &（乱雑位相近似） \end{split} \] \[\epsilon(\mathrm{q})=1+\frac{1}{q^2}\frac{3e^2n_0}{2\epsilon E_F}~~~（トーマスフェルミ近似）\] 両者を比較すると，第二項の形が違うことがわかります．トーマス・フェルミ近似では，化学ポテンシャルが空間的に一定で局所的に伝導帯下端がシフトしていると考えて，誘起電子密度を計算しました．一方で，乱雑位相近似では一次摂動論をベースに誘起電子密度を計算しました．もう少し詳細に説明すると，摂動ポテンシャルにより \(\mathbf{k}\rightarrow \mathbf{k}\pm\mathbf{q}\) の励起が発生します．この励起により，\(\cos\) 型の誘起電子密度が発生します．この \(\cos\) 型の誘起電子密度を全てのケースについて足し合わせたものが上記の結果になります（上図）．

    上記の乱雑位相近似の結果から，\(\mathbf{q}\) が大きいほど遷移確率が低下することがわかります．これは，ポテンシャルが急激に変化する部分には電子は応答できないことを意味します．トーマス・フェルミ近似でも同様のことを話しましたが，乱雑位相近似のほうが直接的に説明できます．

    実は，乱雑位相近似の結果に対し，長波長近似：\(\mathrm{q}\rightarrow 0\) をすると，トーマス・フェルミ近似の結果になります： \[\scriptsize \begin{split} \epsilon(\mathrm{q})&=1+\frac{1}{V}\frac{e^2}{\epsilon q^2}\sum_{\mathbf{k}}\frac{f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))-f(E_0(k))}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)}\\ &=1+\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k}\frac{f(E_0(\left|\mathbf{k}+\mathbf{q}\right|))-f(E_0(k))}{E_0(k)-E_0(\left|\mathbf{k}+\mathbf{q}\right|)} \end{split} \] \(E_0(k)=\frac{\hbar^2k^2}{2m^*}\),
\(E_0(\left|\mathbf{k}+\mathbf{q}\right|)=\frac{\hbar^2}{2m^*}(k^2+2kq\cos\theta+q^2)\)
\(\sim \frac{\hbar^2}{2m^*}(k^2+2kq\cos\theta)\)（長波長近似なので，\(q^2\) を無視）
\(f(\left|\mathbf{k}+\mathbf{q}\right|)\sim f(k)+\mathbf{q}\cdot\nabla f(k)\) \[\scriptsize \begin{split} \epsilon(\mathrm{q}) &=1+\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k}\frac{f(E_0(k))+\mathbf{q}\cdot\nabla f(E_0(k))-f(E_0(k))}{-\frac{\hbar^2}{m^*}\mathbf{k}\cdot\mathbf{q}}\\ &=1-\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k}\frac{\mathbf{q}\cdot\nabla f(E_0(k))}{\frac{\hbar^2}{m^*}\mathbf{k}\cdot\mathbf{q}}\\ &=1-\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k}\frac{\mathbf{q}\cdot\frac{dE_0(k)}{d\mathbf{k}} \frac{d}{dE_0(k)}f(E_0(k))}{\frac{\hbar^2}{m^*}\mathbf{k}\cdot\mathbf{q}}\\ &=1-\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k}\frac{\mathbf{q}\cdot \mathbf{k} \frac{\hbar^2}{m^*} \frac{d}{dE_0(k)}f(E_0(k))}{\frac{\hbar^2}{m^*}\mathbf{k}\cdot\mathbf{q}}\\ &=1-\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k} \frac{d}{dE_0(k)}f(E_0(k))\\ &=1-\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\int d\mathbf{k} \left(-\frac{d}{dE_F}f(E_0(k))\right)\\ &=1+\frac{1}{(2\pi)^3}\frac{e^2}{\epsilon q^2}\frac{d}{dE_F}\int d\mathbf{k} f(E_0(k))\\ &=1+\frac{e^2}{\epsilon q^2}\frac{d}{dE_F}n_0\\ \end{split} \] ここで，絶対零度を仮定すると，\(\frac{d}{dE_F}n_0=\frac{d}{dE_F}\frac{1}{3\pi^2}\left(\frac{2m^*E_F}{\hbar^2}\right)^{\frac{3}{2}}=\frac{3}{2E_F}n_0\) より， \[ \begin{split} \epsilon(\mathrm{q}) &=1+\frac{e^2}{\epsilon q^2}\frac{3}{2E_F}n_0\\ &=1+\frac{1}{q^2}\frac{3e^2n_0}{2\epsilon E_F} \end{split} \] となり，トーマス・フェルミ近似の結果に一致します．本来 \(\mathbf{q}\) が大きいほど遷移確率は下がりますが，そういったあるポテンシャルのフーリエ成分に対する"応答のしやすさ"を無視したものがトーマス・フェルミ近似の結果です．

補足：誘電関数

    誘電関数とは何かを説明します．そのために，少し準備します．線形応答理論では，外場のポテンシャル \(\phi_\mathrm{ext}(\mathrm{r},t)\) と外場と外場によって誘起された電荷のポテンシャル \(\phi_\mathrm{tot}(\mathbf{r},t)\) の関係は， \[ \phi_\mathrm{ext}(\mathbf{r},t)=\int d\mathbf{r'} \int dt' \epsilon(\mathbf{r}-\mathbf{r'},t-t')\phi_\mathrm{tot}(\mathbf{r'},t') \] いわゆる畳み込み積分の形ですね．上の \(\epsilon\) が誘電関数です．しかし，誘電関数は通常フーリエ成分の形で書かれます．上記をフーリエ変換すると，積の形になります（畳み込み積分をフーリエ変換する計算は，よくある計算なので省略）： \[ \phi_\mathrm{ext}(\mathbf{q},\omega)=\epsilon(\mathbf{q},\omega)\phi_\mathrm{tot}(\mathbf{q},\omega) \] 上記の誘電関数は，今回計算で求めたものになります．さらに， \[ \phi_\mathrm{tot}(\mathbf{q},\omega)=\frac{\phi_\mathrm{ext}(\mathbf{q},\omega)}{\epsilon(\mathbf{q},\omega)} \] と変形します．（この形が一番誘電関数を説明しやすい）摂動 \(\phi_\mathrm{ext}(\mathbf{q},\omega)\) が入ってきたときに，電荷が誘起されます．誘電関数は，その誘起電荷によってどの程度外場が変調されるかを表します．率ではなく関数なのは，ポテンシャルの波数や振動数に依存する値だからです．（ちなみに，外場を強める方向になる=誘電関数が1より小さくなる場合もあります．プラズモンで調べてみましょう．）